Algebra of Vectors

Algebra of Vectors

We have studied basic algebraic operations on real numbers and on matrices. Similarly we studied some operations on vectors. Now let us see how to add two vectors, subtract a vector from another vector and multiply a vector by a scalar.

1. Addition of Vectors

Let us define the sum of two vectors in two ways and see that they are the same. Let us assume that an object of unit mass is placed at the origin (0,0) in R2. We assume that the size of the object is just a point. Let us assume that two forces and of unit magnitude act on the object in the positive directions of x-axis and y-axis respectively (Fig.8.4). It is easy to guess that the object will move in the direction 45° to the x-axis as indicated in Fig.8.5. The forces and are equal to the vectors and b as indicated in Fig. 8.6. We may think that the forces push the object in Fig. 8.4 and pull the object in Fig.8.6.

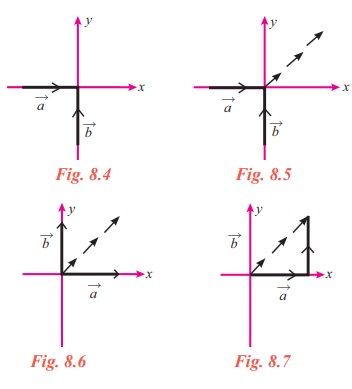
The next question before us is ‘How long will it go?’. Let us assume that the forces act one after the other. The force will move the object one unit along the x-axis. So the object will move from (0, 0) to (1, 0). Now the force will move the object vertically from (1, 0) to (1, 1). So finally the object will be at (1, 1) (Fig. 8.7). Thus the sum of the two vectors may be defined as the line segment joining (0, 0) and (1, 1) in the direction ‘(0, 0) to (1, 1)’.

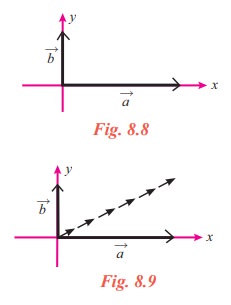
Now, as in the same situation discussed above, let us assume that the force has magnitude 2 instead of 1 (Fig. 8.8). It will not be difficult to guess that the object will move in a direction much closure to the x-axis as indicated in Fig. 8.9. Also we may guess that the object will go to the point (2,1). Thus the sum of the two vectors may be defined as the line segment joining (0,0) and (2,1) in the direction “(0,0) to (2,1)”.

In the two situations discussed above the directions of the forces are perpendicular to each other. This need not be the case in general. Even then we can add the forces by considering one after the other. For example let and be two forces in a plane as shown in Fig. 8.10.

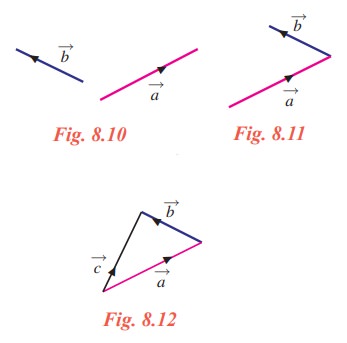
Bringing the initial point of to the terminal point of (Fig. 8.11), we can get the resultant of these two forces (see Fig. 8.12). This motivates us to define the sum of two vectors.

Triangle law of addition

Let and be two vectors. Let A1 and B1 be the initial points of and , and A2 and B2 be the terminal points of and   respectively.

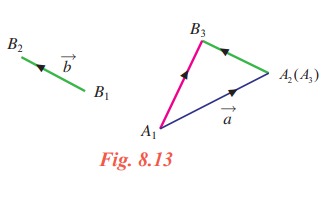
Draw A3 B3 parallel to B1 B2 so that A3 B3 = B1 B2. Then the vector is defined as the sum of the vectors and , and it is denoted as + . This can be restated as,

Definition 8.10 (Triangle law of addition)

If two vectors are represented in magnitude and direction by the two sides of a triangle taken in order, then their sum is represented by the third side taken in the reverse order.

Result 8.1

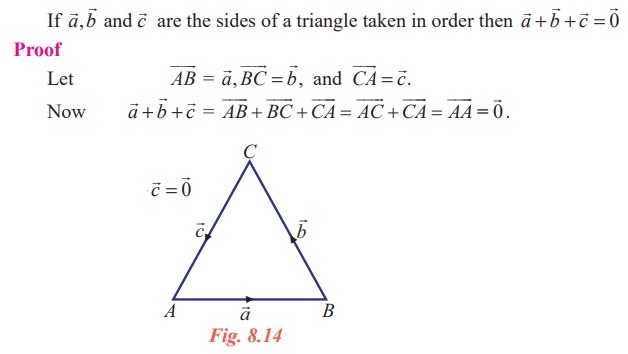
Thus the result is proved.

Parallelogram law of vector addition

Let and be two vectors. Assuming that the initial points of the two vectors are the same, let us find the sum according to Definition 8.7. Let A and B be the terminal points of and respectively (Fig. 8.15). To find + , we draw AC parallel to OB so that OB = AC and declare that is the sum (Fig. 8.16). We observe that OA and BC are parallel (Fig. 8.17).

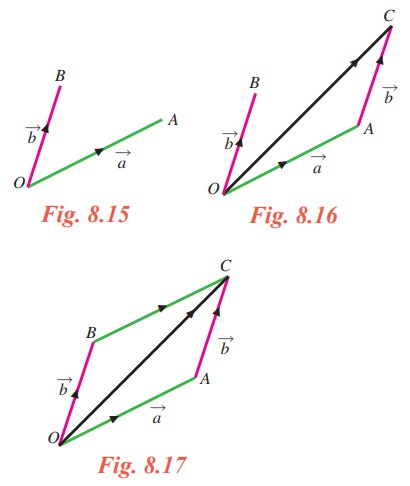
So to find the sum of two vectors with the same initial point, draw the parallelogram with the given vectors as adjacent sides and declare the diagonal as the sum. Even the vectors do not have the same initial point, we can move one of the vectors suitably and make them to have same initial point.

This leads us to the following Definition 8.11.

Let and be two vectors with the same initial point O. Let A and B be the terminal points of and respectively.

Complete the parallelogram OACB. Then the vector is defined as the sum of the vectors and . Thus

Definition 8.11 (Parallelogram law of addition)

In a parallelogram OABC if and represents two adjacent sides, then the diagonal represents their sum (see Fig. 8.17).

Though we have two definitions for addition of vectors, they are one and the same. Definition 8.10 is defined using the triangle law for addition of vectors and Definition 8.11 is defined using the parallelogram law for addition of vectors:

In a triangle ABC if and represent two sides, then the third side represents their sum.

2. Difference between two Vectors

Now let us see how to subtract one vector from another vector.

Definition 8.12

Let be a vector. Then the reverse of , denoted by − , is defined as the vector having the magnitude of and the direction opposite to the direction of .

Notice that if = , then = − .

Geometrical interpretation of difference between two vectors

Thus, if and represent two adjacent sides of a parallelogram then the diagonals represent + and - .

3. Scalar multiplication of a vector

Now let us see how to multiply a vector by a scalar.

Let be a vector and m be a scalar. Then the vector m is called the scalar multiple of a vector  by the scalar m.

Let us note that when m is zero, the magnitude of m becomes 0 and hence m becomes the zero vector. If m is positive, then both a and m a have the same direction and when m is negative, then and m have opposite directions. Thus and m are like vectors if m is positive and unlike vectors if m is negative. The magnitude of m is | m | = | m | | | .

Definition 8.13

Two vectors and are said to be parallel if = λ , where λ is a scalar. If λ > 0 , they are in the same direction. If λ < 0 then they are in the opposite direction to each other.

4. Some properties and results

For any two vectors and and scalars m and n, we have

Proof

Let and be two vectors. Let = , = . Complete the parallelogram OACB with and as adjacent sides. The vectors and have same direction and equal magnitude; so = . Thus 

Polygon law of addition

Let be any five vectors as shown in the Fig. 8.22.

We observe from the figure that each vector is drawn E from the terminal point of its previous one. By the triangle law,

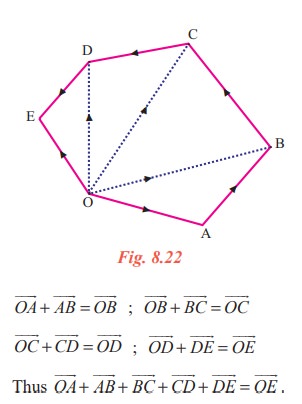
Thus the line joining the initial point of first vector to the terminal point at the last vector is the sum of all the vectors. This is called the polygon law of addition of vectors.

Example 8.1

Represent graphically the displacement of

(i) 30 km 60º west of north

(ii) 60 km 50º south of east.

Solution