Chapter: 11th Mathematics : UNIT 8 : Vector Algebra I
Scalar product and Properties of Scalar Product
Scalar product
Definition 8.16
Let ![]() and
and ![]() be any two non-zero vectors and θ be the included angle of the vectors as in Fig. 8.34.
be any two non-zero vectors and θ be the included angle of the vectors as in Fig. 8.34.
Their scalar product or dot product is denoted by ![]() and
and ![]() is defined as a scalar |
is defined as a scalar | ![]() .
. ![]() | |
| |![]() | cosθ .
| cosθ .
Thus ![]() ⋅
⋅![]() = |
= | ![]() | |
| |![]() | cosθ .
| cosθ .
Since the resultant of ![]() ⋅
⋅ ![]() is a scalar, it is called scalar product. Further we use the symbol dot (‘.’) and hence another name dot product.
is a scalar, it is called scalar product. Further we use the symbol dot (‘.’) and hence another name dot product.
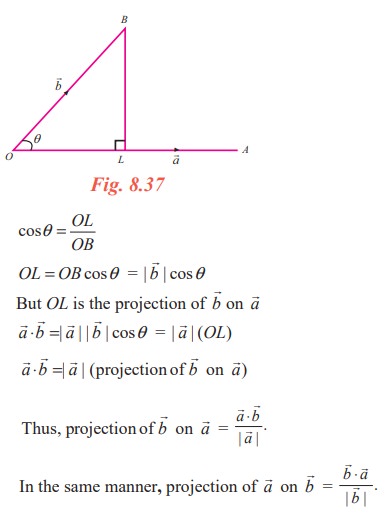
Geometrical meaning of scalar product (projection of one vector on another vector)
Let ![]() =
= ![]() ,
, ![]() =
= ![]() and θ be the angle between
and θ be the angle between ![]() and
and ![]() .
.
Draw BL perpendicular to OA. From the right triangle OLB
cosθ = OL/OB
Properties of Scalar Product
(i) Scalar product of two vectors is commutative.
With usual definition,
![]() ⋅
⋅ ![]() = |
= | ![]() | |
| | ![]() |cosθ = |
|cosθ = | ![]() | |
| | ![]() |cosθ =
|cosθ = ![]() ⋅
⋅ ![]()
That is, for any two vectors ![]() and b ,
and b ,
![]() ⋅
⋅ ![]() =
= ![]() ⋅
⋅![]() .
.
(ii) Nature of scalar product
We know that 0 ≤ θ ≤ π .

Proof





Note 8.5
Suppose three sides are given in vector form, prove
(i) either sum of the vectors is ![]() or sum of any two vectors is equal to the third vector, to form a triangle.
or sum of any two vectors is equal to the third vector, to form a triangle.
(ii) dot product between any two vectors is 0 to ensure one angle is p/2 .
EXERCISE 8.3

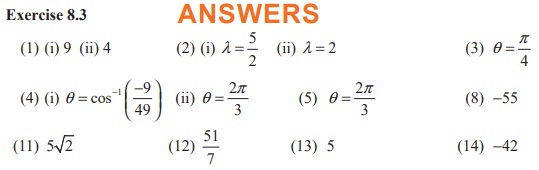
Related Topics