Resolution of Vectors

Resolution of Vectors

Resolution of a vector can be done for any finite dimension. But we will discuss only in two and three dimensions. Let us start with two dimension.

Resolution of a vector in two dimension

Theorem 8.5

Let iˆ and ˆj be the unit vectors along the positive x-axis and the y-axis having initial point at the origin O. Now is the position vector of any point P in the plane. Then can be uniquely written as

= xiˆ + y jˆ for some real numbers x and y. Further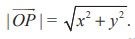

Proof

Let (x, y) be the coordinates of the point P. Let L and M be the foots of the perpendiculars drawn from P to the x and y axes. Then

To prove the uniqueness, let x1iˆ + y1 ˆj and x2 iˆ + y2 ˆj be two representations of the same point P. Then

x1iˆ + y1jˆ = x2iˆ + y2jˆ .

This implies that

(x1 − x2 )iˆ − ( y2− y1 ) ˆj = ⇒ x1 − x2 = 0, y2 − y1 = 0.

In other words x1 = x2  and y1 = y2  and hence the uniqueness follows.

In the triangle OLP, OP2 = OL2 + LP2 ;

hence | |=  √[ x2 + y2 ].

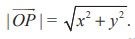
That is,

Observe that if iˆ + jˆ are the unit vectors in the postive directions of x and y axes, then the  iˆ and jˆ position vector of the point (6,4) can be written as 6iˆ + 4 jˆ  and this is the only way of writing it.

Result 8.8

If and are two non-collinear vectors in a plane, then any vector in the plane can be written as the linear combination of and in a unique way. That is, any vector in the plane is of the form l + m for some scalars l and m.

Proof

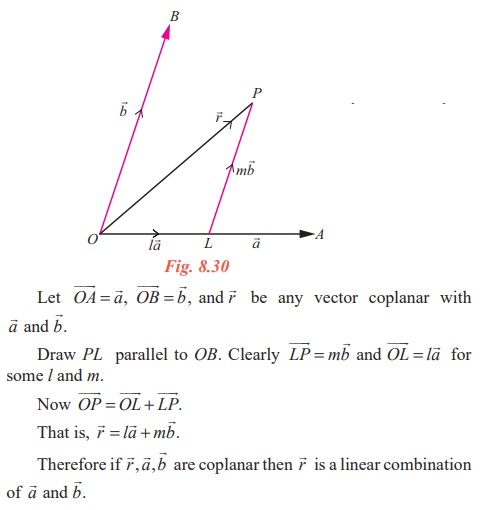
Note 8.2

Further if three non collinear vectors are coplanar then any one of the vector can be written as a linear combination of other two. Note that the converse is also true.

Result 8.9

If , and are three non-coplanar vectors in the space, then any vector in the space can be written as l + m + n in a unique way for some scalars l, m and n.

Definition 8.15

Let iˆ and ˆj be the unit vectors in the positive directions of x and y axes respectively. Let be any vector in the plane. Then = xiˆ + y ˆj for some real numbers x and y. Here xiˆ and y ˆj are called the rectangular components of along the x and y axes respectively in two dimension.

What we discussed so far can be discussed in the three dimensional space also.

Resolution of a vector in three dimension

Theorem 8.6

Let iˆ, ˆj and kˆ be the unit vectors in the direction of postive x, y and z axes respectively having initial point at the origin O. Let be the position vector of any point P in the space. Then can be uniquely written as = xiˆ + y ˆj + zkˆ for some real numbers x, y and z. Further | | = √ [ x 2+ y 2 + z2 ].

Proof

Let (x, y, z) be the coordinates of the point P. Let Q be the foot of the perpendicular drawn from P to the xy-plane. Let R and S be the foots of the perpendiculars drawn from Q to the x and y axes respectively. Let = .

Then, OR = x, OS = y, and QP = z. z

Components of vector joining two points

Let us find the components of the vector joining the point  (x1 , y1 ) to (x2 , y2 ).

Let A and B be the points (x1 , y1 ) and (x2 , y2 ). Let P be the point (x2 − x1 , y2 − y1 ). Then  =.

The components of are  (x2 − x1 )iˆ and ( y2 − y ) jˆ. Hence the components of in the directions of x and y axes are (x2 − x1 )iˆ ( y2 − y1 ) jˆ.

Similarly if A and B are the points (x1 , y1 , z1 ) and (x2 , y2 , z2 ), then the components of in the directions of x, y and z axes are (x2 − x1)iˆ ( y2 − y1 ) jˆ (z2 − z1 )kˆ .

Matrix representation of a vector

A vector with three components can be visualised as either a row or column matrix as [x, y, z] or respectively.

Thus any vector = a1iˆ + a2 jˆ + a3kˆ can be obtained from

Hence addition of vectors and multiplication of a vector by a scalar can be defined as follows.

k = ka1iˆ + ka2 ˆj + ka3 kˆ

For k ∈ R, k > 1 yields magnification, 0 < k < 1 yields contraction of a vector and k = 0 yields a zero vector = 0iˆ + 0 ˆj + 0kˆ = .

Result 8.10

Using the commutative, associative properties of vector addition and the distributive property of the scalar multiplication we can prove the following.

Example 8.4

Find a unit vector along the direction of the vector 5iˆ − 3 ˆj + 4kˆ.

Note 8.3

Now we have another unit vector parallel to 5iˆ − 3 ˆj + 4kˆ in the opposite direction. That is,