Definition, Theorem, Solved Example Problems | Mathematics - Position vectors | 11th Mathematics : UNIT 8 : Vector Algebra I
Chapter: 11th Mathematics : UNIT 8 : Vector Algebra I
Position vectors
Position vectors
Definition 8.14
Let O be the origin and P be any point (in the plane or space). Then the vector ![]() is called the position vector of the point P with respect to the origin O (point of reference).
is called the position vector of the point P with respect to the origin O (point of reference).
The relation between the vectors and position vectors are given in the following result.
Result 8.6
Let O be the origin, A and B be two points. Then 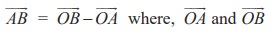 are position vectors of A and B respectively.
are position vectors of A and B respectively.
Proof
We know that,  .
.
Theorem 8.1 (Section Formula - Internal Division)
Let O be the origin. Let A and B be two points. Let P be the point which divides the line segment AB internally in the ratio m : n. If ![]() and
and ![]() are the position vectors of A and B, then the position vector
are the position vectors of A and B, then the position vector ![]() of P is given by
of P is given by
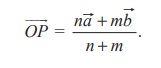
Proof

Theorem 8.2 Section Formula - External Division (Without proof)
Let O be the origin. Let A and B be two points. Let P be the point which divides the line segment AB externally in the ratio m : n. If ![]() and
and ![]() are the position vectors of A and B, then the position vector
are the position vectors of A and B, then the position vector ![]() of P is given by
of P is given by
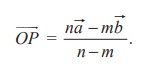
Note 8.1
By taking m = n = 1 in Theorem 8.1, we see that the position vector of the midpoint of the line joining the points A and B is ![]() +
+![]() / 2 , where
/ 2 , where ![]() and
and ![]() are the position vectors of the points A and B respectively.
are the position vectors of the points A and B respectively.
From the above theorem we can get a condition for three points to be collinear.
Result 8.7
Three distinct points A, B and C with position vectors ![]() ,
, ![]() and
and ![]() are collinear if and only if there exist real numbers x,y,z, none of them is zero, such that
are collinear if and only if there exist real numbers x,y,z, none of them is zero, such that
x + y + z = 0 and x![]() + y
+ y![]() + z
+ z![]() = 0.
= 0.

Let us recall the definition that the line joining a vertex of a triangle with the midpoint of its opposite side is called a median. The centroid divides the median from vertex to the midpoint of the opposite side internally in the ratio 2:1.
Theorem 8.3
The medians of a triangle are concurrent.
Proof
Let ABC be a triangle and let D, E, F be the mid points of its sides BC, CA and AB respectively.
We have to prove that the medians AD, BE, CF are concurrent.
Let O be the origin and ![]() ,
,![]() ,
, ![]() be the position vectors of A, B, and C respectively.
be the position vectors of A, B, and C respectively.
The position vectors of D, E, and F are respectively
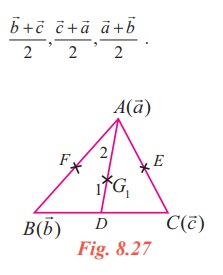
Let G1 be the point on AD dividing it internally in the ratio 2 : 1

From (1), (2), and (3) we find that the position vectors of the three points G1, G2, G3 are one and the same. Hence they are not different points. Let the common point be G.
Therefore the three medians are concurrent and the point of concurrence is G.
Theorem 8.4
A quadrilateral is a parallelogram if and only if its diagonals bisect each other.
Proof
Let A, B, C, D be the vertices of a quadrilateral with diagonals AC and BD. Let ![]() ,
, ![]() ,
, ![]() and
and ![]() be the position vectors of A, B, C, and D respectively with respect to O.
be the position vectors of A, B, C, and D respectively with respect to O.
Let the quadrilateral ABCD be a parallelogram. Then

This shows that the position vectors of the midpoint of the line segments AC and BD are the same. In other words, the diagonals bisect each other.
Conversely let us assume that the diagonal bisects each other. Thus the position vectors of the midpoint of the line segments AC and BD are the same. Thus
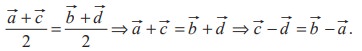
This implies that 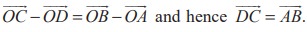 . This shows that the lines AB and DC are parallel. From
. This shows that the lines AB and DC are parallel. From ![]() +
+ ![]() =
= ![]() +
+ ![]() we see that
we see that ![]() −
− ![]() =
= ![]() −
− ![]() which shows that the lines AD and BC are parallel. Hence ABCD is a parallelogram.
which shows that the lines AD and BC are parallel. Hence ABCD is a parallelogram.
EXERCISE 8.1
(1) Represent graphically the displacement of
(i) 45cm 30º north of east. (ii) 80km, 60 º south of west
(2) Prove that the relation R defined on the set V of all vectors by ![]() R
R ![]() if
if ![]() =
=![]() ' is an equivalence relation on V.
' is an equivalence relation on V.
(3) Let ![]() and
and ![]() be the position vectors of the points A and B. Prove that the position vectors of the points which trisects the line segment AB are
be the position vectors of the points A and B. Prove that the position vectors of the points which trisects the line segment AB are
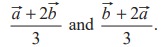
(4) If D and E are the midpoints of the sides AB and AC of a triangle ABC, prove that
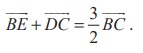
(5) Prove that the line segment joining the midpoints of two sides of a triangle is parallel to the third side whose length is half of the length of the third side.
(6) Prove that the line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.
(7) If ![]() and
and ![]() represent a side and a diagonal of a parallelogram, find the other sides and the other diagonal. Answer: Other sides
represent a side and a diagonal of a parallelogram, find the other sides and the other diagonal. Answer: Other sides ![]() -
- ![]() , -
, - ![]() ,
, ![]() -
- ![]() and other diagonal
and other diagonal ![]() -2
-2 ![]()
(8) If  , prove that the points P, Q, R are collinear.
, prove that the points P, Q, R are collinear.
(9) If D is the midpoint of the side BC of a triangle ABC, prove that 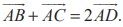
(10) If G is the centroid of a triangle ABC, prove that 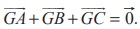
(11) Let A, B, and C be the vertices of a triangle. Let D,E, and F be the midpoints of the sides BC, CA, and AB respectively. Show that 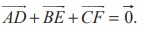
(12) If ABCD is a quadrilateral and E and F are the midpoints of AC and BD respectively, then prove that
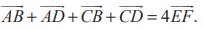
Related Topics