Definition, Illustration, Example, Solution | Mathematics - Types of Functions | 10th Mathematics : UNIT 1 : Relation and Function
Chapter: 10th Mathematics : UNIT 1 : Relation and Function
Types of Functions
Types of Functions
In this section, we
will discuss the following types of functions with suitable examples.
(i) one – one
(ii) many – one
(iii) many – one
(iv) into
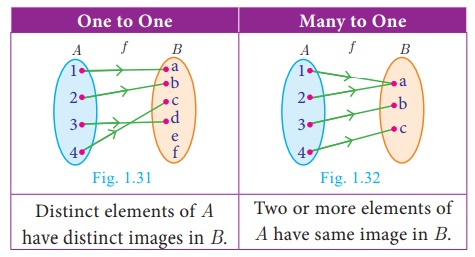
1. One – one function
Let us assume that we
have a cell phone with proper working condition. If you make a usual call to
your friend then you can make only one call at a time (Fig.1.21).
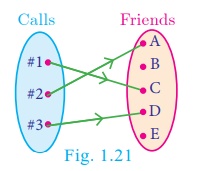
If we treat making
calls as a function, then it will be one – one.
A function f : A→ B is called one – one function if distinct elements
of A have distinct images in B.
A one-one
function is also called an injection.
Equivalently,
If for all a1, a2 ∈ A , f (a1) = f (a2 ) implies a1 =
a2 , then f is called one – one function.
Illustration 10
A = {1,2,3,4} and B =
{a,b,c,d,e}
(i) Let f =
{(1,a), (2,b), (3,d), (4,c)}
In Fig. 1.22, for different elements in A, there are different images in B.
Hence f is a
one – one function.

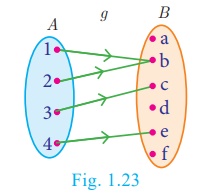
(ii) Let g =
{(1,a), (2,b), (3,c), (4,e)}
g is a function from A to B
such that g(1) = g(2)
= b , but 1 ≠ 2.
Thus two distinct
elements 1 and 2 in the first set A have same image b the second
set in B (Fig.1.23). Hence, g is not a one–one function.
2. Many – one function
In a theatre complex
three films F1,
F2 , F3 are shown. Seven persons (P1 to P 7)
arrive at the theatre
and buy tickets as shown (Fig 1.24).
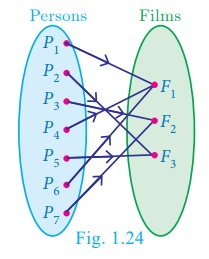
If the selection of
films is considered as a relation, then this is a function which is many–one, since more
than one person may choose to watch the same film.
A function f
: A→ B is called many-one
function if two or more elements of A
have same image in B.
In other words, a
function f: A→ B is called many-one if f it is not
one–one.
Illustration 11
Let A =
{1,2,3,4} and ; Let f = {(1,a), (2,a), (3,b), (4,c)}
Then f is a
function from A to B in which different elements 1 and 2 of A have
the same image a in B. Hence f is a many – one function.
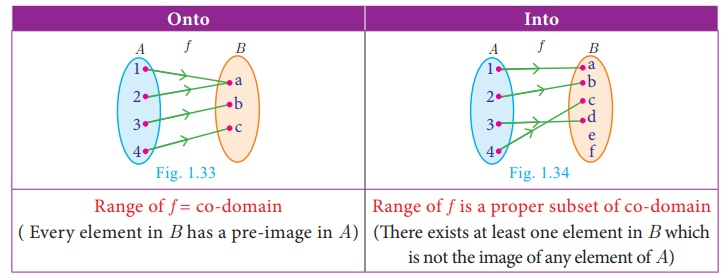
3. Onto function
In a mobile phone
assume that there are 3 persons in the contact. If every person in the contact
receives a call, then the function representing making calls will be onto.
(Fig.1.25)
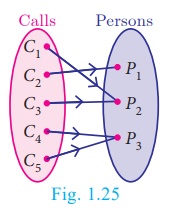
A function f
: A→ B is said to be onto
function if the range of f is
equal to the co-domain of f.
In other words, every
element in the co-domain B has a pre-image in the domain A. An
onto function is also called a surjection.
note
If f : A → B is an
onto function then, the range of f =
B . That is, f (A) = B .
Illustration 12
Let A = {x,y,
z}, B = {l,m,n} ;
Range of f = {l,m,n}
= B (Fig.1.26)
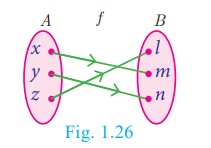
Hence f is an onto function.
4. Into function
In a home appliance
showroom, the products television, air conditioner, washing machine and water
heater were provided with 20% discount as new year sale offer. If the selection
of the above products by the
three customers C1, C2, C3 is considered as a
function then the following diagram (Fig.1.27) will represent an into function.
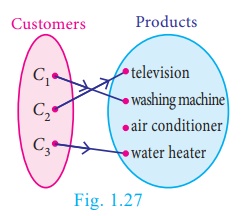
During winter season
customers usually do not prefer buying air conditioner. Here air conditioner is
not chosen by any customer. This is an example of into function.
A function f
: A→ B is called an into
function if there exists atleast one element in B which is not the image of any element of A.
That is the range of f
is a proper subset of the co-domain of f.
In other words, a
function f: A→ B is called ‘into’ if it is not ‘onto’.
Illustration 13
Let A = {1,2,3,}
and B = {w, x,y, z} ; f =
{(1,w),(2, z),(3,x)}
Here, range of f
= {w, x, z} ⊂ B (Fig.1.28)
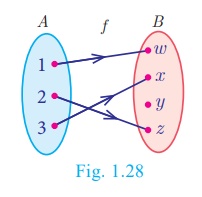
Therefore, f is
a into function.
Note that y ∈ B is not an image of any element in A.
5. Bijection
Consider the circle
where each letter of the English alphabet is changed from
inner portion to a
letter in the
outer portion.
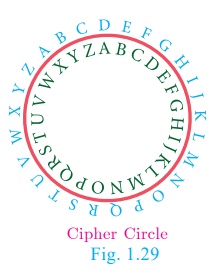
Thus A → D
, B → E , C → F , … Z → C
. We call this circle as‘cipher circle’. (Fig.1.29) In this way if we try
to change the word‘HELLO’ then it will become ‘KHOOR’. Now using the same
circle if we substitute for each outer
letter the corresponding inner letter we will get back the word ‘HELLO’. This
process of converting
from one form to an other form and receiving back
the required information is called bijection. This process is widely used in the study of secret
codes called ‘cryptography’.
If a function f : A→ B is both one–one and onto,
then f is called a bijection from A to B.
Illustration 14

Illustration 15
Note
A one – one and onto
function is also called a one – one correspondence.
To determine whether
the given function is one–one or not the following test may help us.
6. Horizontal Line Test
Previously we have
seen the vertical line test. Now let us see the horizontal line test. “A function represented in a graph is
one–one, if every horizontal line intersects the curve in at most one point”.
Example 1.12
Using horizontal line
test (Fig.1.35(a), 1.35(b), 1.35(c)), determine which of the following
functions are one – one.

Solution
The curves in
Fig.1.35(a) and Fig.1.35(c) represent a one–one function as the horizontal
lines meet the curves in only one point P.
The curve in
Fig.1.35(b) does not represent a one–one function, since, the horizontal meet
the curve in two points P and Q.
Example 1.13 Let A =
{1, 2, 3} , B = {4, 5, 6, 7} and f = {(1,
4),(2, 5),(3, 6)} be a function from A to B. Show that f is
one – one but not onto function.
Solution A = {1, 2, 3} , B =
{4, 5, 6, 7} ; f = {(1, 4),(2, 5),(3, 6)}

Then f is a function from A to B and for different elements in A, there are different images in B. Hence f is one–one function. Note that the element 7 in the co-domain does not have any pre-image in the domain. Hence f is not onto (Fig.1.36).
Therefore f is
one–one but not an onto function.
Example 1.14 If A =
{−2,−1, 0,1, 2} and f: A→ B
is an onto function defined by f (x) = x2 + x
+ 1 then find B.
Solution Given A =
{−2,−1, 0,1, 2} and f (x) = x2 + x
+ 1 .
f (-2) = (−2)2
+ (−2) + 1 =3; f (-1) = (−1)2 + (−1) + 1 =1
f (0) = 02 +
0 + 1 =1;
f (1) = 12 + 1
+ 1 = 3
f (2) =22 +
2+ 1 = 7
Since, f is an
onto function, range of f = B = co-domain of f.
Therefore, B =
{1, 3, 7}.
Example 1.15 Let f
be a function f : N → N be defined by f (x) = 3x + 2, x ∈ N
(i) Find the images of
1, 2, 3
(ii) Find the pre-images
of 29, 53
(iii) Identify the
type of function
Solution
The function f :
N → N is defined by f (x)
= 3x + 2
(i) If x =
1, f (1) = 3(1) + 2 = 5
If x = 2, f (2)
=3(2) + 2 = 8
If x = 3 , f
(3) = 3(3) + 2 = 11
The images of 1, 2, 3
are 5, 8, 11 respectively.
(ii) If x is
the pre-image of 29, then f (x) = 29 . Hence 3x + 2 = 29
3x = 27 ⇒ x = 9.
Similarly, if x is
the pre-image of 53, then f (x) = 53 . Hence 3x + 2 = 53 3x
= 51 ⇒ x = 17
Thus the pre-images of
29 and 53 are 9 and 17 respectively.
(iii) Since different
elements of N have different images in the co-domain, the function f is
one – one function.
The co-domain of f is
N.
But the range of f =
{5, 8, 11, 14, 17, ...} is a proper subset of N.
Therefore f is
not an onto function. That is, f is an into function. Thus f is
one – one and into function.
Example 1.16
Forensic scientists
can determine the height (in cms) of a person based on the length of their
thigh bone. They usually do so using the function h(b) = 2 ⋅ 47b + 54 ⋅ 10 where b is
the length of the thigh bone.
(i) Check if the
function h is one – one
(ii) Also find the
height of a person if the length of his thigh bone is 50 cms.
(iii) Find the length
of the thigh bone if the height of a person is 147 × 96 cms.
Solution
(i) To check if h is
one – one, we assume that h(b1) = h(b2)
Then we get, 2 ⋅ 47b1 + 54 ⋅ 10 = 2 ⋅ 47b2 + 54 ⋅ 10
2 × 47b1
= 2 ⋅ 47b2 ⇒ b1
= b2
Thus, h(b1)
= h(b2) ⇒ b1
= b2. So, the function h is one – one.
(ii) If the length of
the thigh bone b = 50, then the height is
h(50) = (2 ⋅ 47 × 50) + 54 ⋅ 10 = 177 ⋅ 6 cms.
(iii) If the height of
a person is 147 × 96 cms, then h(b) = 147 ⋅ 96 and so the length of the thigh bone is given by 2 ⋅ 47b + 54 ⋅ 10 = 147 ⋅ 96 .
b = [ 93 ⋅ 86 / 2 ⋅ 47 ] = 38
Therefore, the length of the thigh bone is 38 cms.
Related Topics