Identifying the graphs of Linear, Quadratic, Cubic and Reciprocal functions

Identifying the graphs of Linear, Quadratic, Cubic and Reciprocal functions

Graphs provide visualization of curves and functions. Hence, graphs help a lot in understanding the concepts in a much efficient way.

In this section, we will be discussing about the identification of some of the functions through their graphs. In particular, we discuss graphs of Linear, Quadratic, Cubic and Reciprocal functions.

1. Linear Function

A  function  f  : R → R defined by f (x) = mx + c , m ≠ 0 is called a linear function. Geometrically this represents a straight line in the graph.

Some Specific Linear Functions and their graphs are given below.

2. Modulus or Absolute valued Function

f  : R → [0, ∞) defined by  f (x) =| x | 

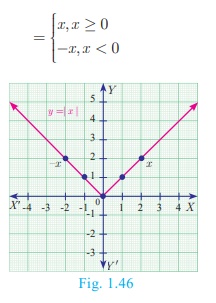
Note

·           Modulus function is not a linear function but it is composed of two linear functions xand –x.

·           Linear functions are always one-one functions and has applications in Cryptography as well as in several branches of Science and Technology.

3. Quadratic Function

A function f : R → R defined by f (x) = ax² + bx + c, (a ≠ 0) is called a quadratic function

Some specific quadratic functions and their graphs

The equations of motion of a particle travelling under the influence of gravity is a quadratic function of time. These functions are not one – one.  (Why?)

4. Cubic Function

A function f : R → R defined by f (x) = ax³ + bx² + cx + d,(a ≠ 0) is called a cubic function. The graph of f (x) = x³ is shown in Fig.1.48.

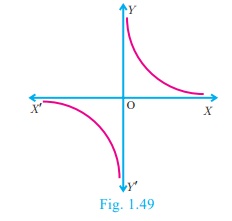
5. Reciprocal Function

A function f : R − {0} → R defined by f (x) = 1/x is called a reciprocal function (Fig.1.49).

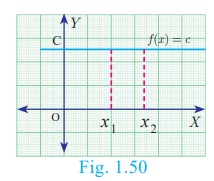
6. Constant Function

A function f : R → R defined by f (x) = c, for all x ∈ R is called a constant function (Fig.1.50).