Exercise 1.5: Composition of Functions

Exercise 1.5

1. Using  the functions f  and  g  given  below, find f o g and g o f . Check whether f o g = g o f.

(i) f (x) = x − 6, g(x) = x2

(ii) f (x) = 2/x, g(x) = 2x2 – 1

(iii) f (x) =  g(x) = 3 – x

(iv) f (x) = 3 + x, g(x) = x – 4

(v) f (x) = 4x2 − 1, g(x) = 1 + x

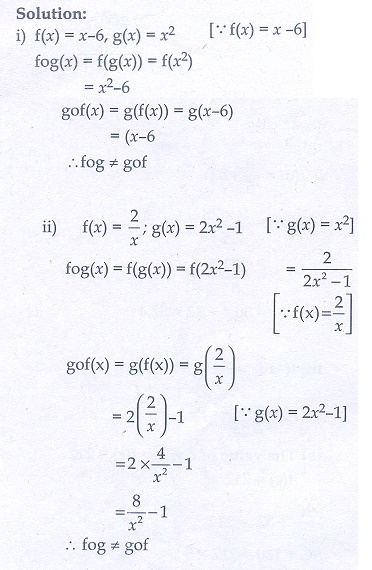
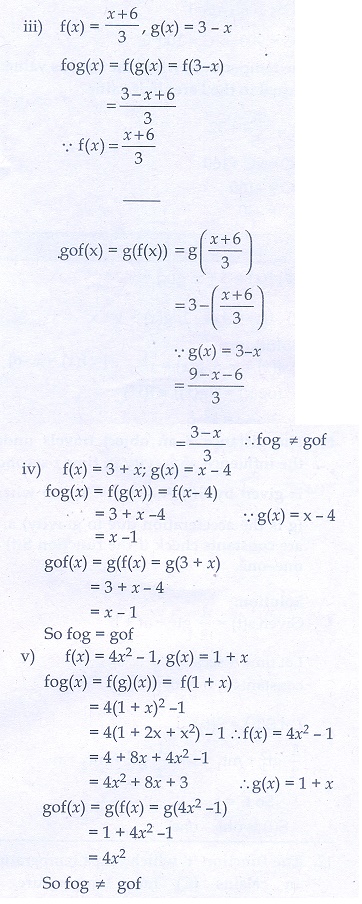
2. Find the value of k, such that f o g = g o f

(i) f (x) = 3x + 2, g(x) = 6x – k

(ii) f (x) = 2x − k, g(x) = 4x + 5

3. If f (x) = 2x − 1, g(x) = [x+1]/2 show that f o g = g o f = x

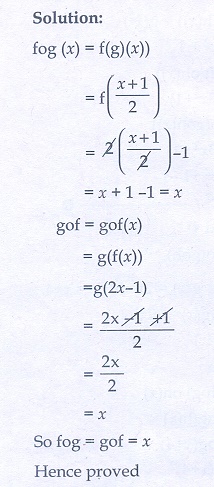
4. (i) If f (x) = x2 − 1, g(x) = x − 2 find a, if g o f (a) = 1.

(ii) Find k, if f (k) = 2k − 1 and f o f (k) = 5 .

5. Let A, B,C ⊆ N and a function f : A → B be defined by f (x) = 2x + 1 and g : B → C be defined by g(x) = x2 . Find the range of f o g and g o f .

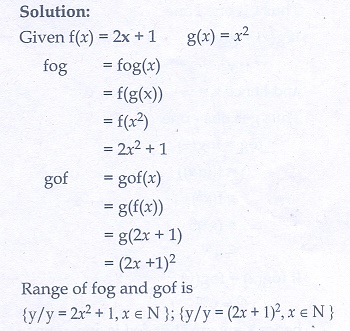
6. Let f (x) = x2 − 1 . Find (i) f o f (ii) f o f o f

7. If f : R → R and g : R → R are defined by f (x) = x5 and g(x) = x4 then check if f, g are one-one and f o g is one-one?

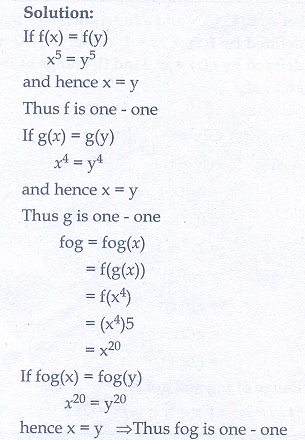
8. Consider the functions f (x), g(x), h(x) as given below. Show that

(f o g) o h = f o (g o h) in each case.

(i) f (x) = x − 1, g(x) = 3x + 1 and h(x) = x2

(ii) f (x) = x2, g(x) = 2x and h(x) = x + 4

(iii) f (x) = x − 4, g(x) = x2 and h(x) = 3x – 5

9. Let f = {(−1, 3),(0,−1),(2,−9)} be a linear function from Z into Z. Find f (x).

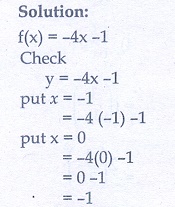
10. In electrical circuit theory, a circuit C(t) is called a linear circuit if it satisfies the superposition  principle  given  by  C (at1 + bt2 ) = aC (t1) + bC(t2),  where  a,b are constants. Show that the circuit C (t) = 3t is linear.

Answers: