Representation of Functions

Representation of Functions

A function may be represented by

(a) a set of  ordered pairs

(b) a table form

(c) an arrow diagram

(d) a graphical form

Let f: A→ B be a function

(a) Set of ordered pairs

The set f= {(x,y) | y = f (x), x ∈ A} of all ordered pairs represent a function.

(b) Table form

The values of x and the values of their respective images under f can be given in the form of a table

(c) Arrow diagram

An arrow diagram indicates the elements of the domain of f and their respective images by means of arrows

(d) Graph

The ordered pairs in the collectionf= {(x,y)| y = f (x), x ∈ A} are plotted as points in the xy- plane. The graph of f is the totality of all such points’

Every function can be represented by a curve in a graph. But not every curve drawn in a graph will represent a function.

The following test will help us in determining whether a given curve is a function or not.

Vertical line test

“A curve drawn in a graph represents a function, if every vertical line intersects the curve in at most one point.”

Example 1.10

Using vertical line test, determine which of the following curves (Fig.1.18(a), 1.18(b), 1.18(c), 1.18(d)) represent a function?

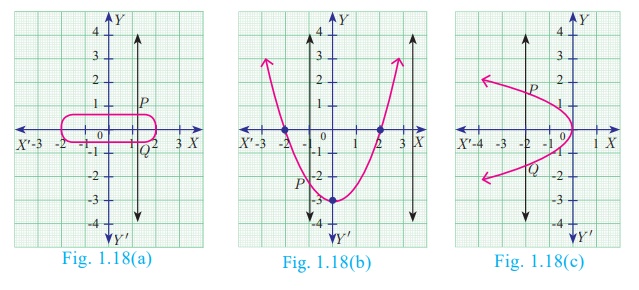
Solution

The curves in Fig.1.18(a) and Fig.1.18(c) do not represent a function as the vertical lines meet the curves in two  points P and Q.

The curves in Fig.1.18(b) and Fig.1.18(d) represent a function as the vertical lines meet the curve in at most one point.

Notes

Any equation represented in a graph is usually called a ‘curve’.

Example 1.11 Let  A = {1, 2, 3, 4} and  B = {2, 5, 8,11,14}be two sets. Let f: A→ B be a function given by f (x) = 3x − 1 . Represent this function

(i) by arrow diagram

(ii) in a table form

(iii) as a set of ordered pairs

(iv) in a graphical form

Solution

A = {1, 2, 3, 4} ; B = {2, 5, 8,11,14} ;  f (x) = 3x – 1

f (1) = 3(1) – 1 = 3 – 1 = 2 ; f (2) = 3(2) – 1 = 6 – 1 = 5

f (3) = 3(3) – 1 = 9 – 1 = 8 ; f (4) = 4(3) – 1 = 12 – 1 = 11

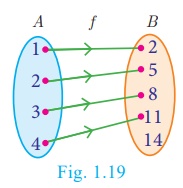
(i) Arrow diagram

Let  us  represent  the  function : A → B by an arrow diagram (Fig.1.19).

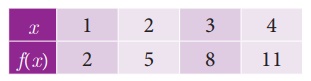
(ii) Table form

The given function f can be represented in a tabular form as given below

(iii) Set of ordered pairs

The function f can be represented as a set of ordered pairs as

f = {(1,2),(2,5),(3,8),(4,11)}

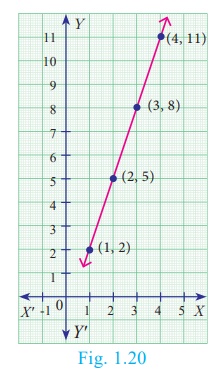
(iv) Graphical form

In the adjacent xy -plane the points

(1,2), (2,5), (3,8), (4,11) are plotted (Fig.1.20).