Definition, Illustration, Example, Solution | Mathematics - Composition of Functions | 10th Mathematics : UNIT 1 : Relation and Function
Chapter: 10th Mathematics : UNIT 1 : Relation and Function
Composition of Functions
Composition of Functions
When a car driver
depresses the accelerator pedal, it controls the flow of fuel which in turn influences
the speed of the car. Likewise, the
composition of two functions is a
kind of ‘chain reaction’, where the functions act upon one after another
(Fig.1.40).
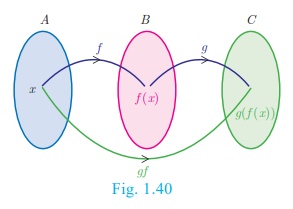
We can explain this
further with the concept that a function is a ‘process’. If f and g are
two functions then the composition g(f (x)) (Fig.1.41) is
formed in two steps.
(i) Feed an input (say
x) to f ;
(ii) Feed the output f(x)
to g to get g(f (x)) and call it gf(x).
Illustration
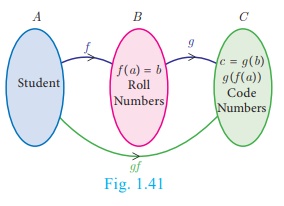
Consider the set A of
all students, who appeared in class X of Board Examination. Each student
appearing in the Board Examination is assigned a roll number. In order to have confidentiality, the Board
arranges to deface the roll number of each student and assigns a code number to
each roll number.
Let A be the
set of all students appearing for the board exam. B ⊆ N be the set all roll numbers and C ⊆ N be the set of all code numbers (Fig.1.41). This gives rise to
two functions f: A → B and g : B → C given
by b = f (a) be the roll number assigned to student a,
c = g(b) be the code number assigned to roll number b,
where a ∈ A , b ∈ B and c ∈ C.
We can write c =
g(b) = g(f (a)).
Thus, by the
combination of these two functions, each student is eventually attached a code
number. This idea leads to the following definition.
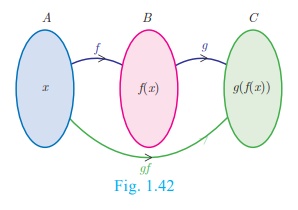
Definition
Let f : A
→ B and g : B → C be two functions (Fig.1.42).
Then the composition of f and g denoted by g o f is defined as the function g o f
(x ) = g( f
(x )) for all x ∈ A .
Example 1.20
Find f o g and g o f when f (x) = 2x +
1 and g(x) = x2 – 2
Solution
f (x) = 2x +
1 , g(x) = x2 – 2
f o g(x) = f (g(x))
= f (x2 − 2) = 2(x2 − 2) + 1 = 2x2
– 3
g o f (x) = g(f (x))
= g(2x + 1) = (2x + 1)2 − 2 = 4x2
+ 4x – 1
Thus f o g = 2x2 − 3, g o f = 4x2 + 4x − 1. From the above, we see that f o g ≠ g o f .
Note
Generally, f o g ≠ g o f
for any two functions f and g. So, composition of functions is
not commutative.
Example 1.21
Represent the function
f (x) = 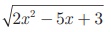 as a composition of two functions.
as a composition of two functions.
Solution
We set f (x)
= 2x2 − 5x + 3 and f (x) = √x
Then,
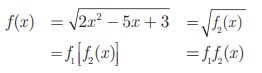
Example 1.22
If f (x)
= 3x − 2 , g(x) = 2x + k and if f o g = g o f , then find
the value of k.
Solution
f (x) = 3x −
2 , g(x) = 2x + k
f o g(x) = f (g(x))
= f (2x + k) = 3(2x + k) − 2 = 6x + 3k
– 2
Thus, f o g(x) = 6x + 3k –
2.
g o f (x) = g(3x − 2)
= 2(3x − 2) + k
Thus, g o f (x) = 6x − 4 + k .
Given that f o g = g o f
Therefore, 6x +
3k − 2 = 6x − 4 + k
6x − 6x +
3k − k = −4 + 2 ⇒ k = −1
Example 1.23
Find k if f o f (k) = 5 where f (k)
= 2k – 1.
Solution
f o f (k) = f (f (k))
= 2(2k − 1) − 1
= 4k − 3
Thus, f o f (k) = 4k – 3
But, it is given that f
o f (k) =
5
Therefore 4k -
3 = 5 ⇒ k = 2 .
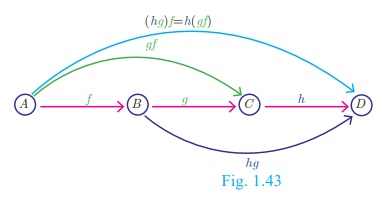
Composition of three functions
Let A,
B, C, D be four sets and let f : A → B ,
g : B → Cand h : C → D
be three functions (Fig.1.43). Using composite functions f o g and g o h , we get two new functions
like (f o g) o h and f o (g o h).
We observed that the
composition of functions is not commutative. The natural question is about the
associativity of the operation.
Note
Composition of three
functions is always associative. That is, f o (g o h) = (f o g) o h
Example 1.24
If f (x)
= 2x + 3 , g(x) = 1 − 2x and h(x) = 3x .
Prove that f o (g o h) = (f o g) o h
Solution
f (x) = 2x +
3 , g(x) = 1 − 2x , h(x) = 3x
Now, (f o g)(x) = f (g(x))
= f (1 − 2x) = 2(1 − 2x) + 3 = 5 − 4x
Then, (f o g) o h(x) = (f o g)(h(x)) = (f o g)(3x) = 5 − 4(3x) = 5 −
12x ……… (1)
(g o h)(x) = g(h(x))
= g(3x) = 1 − 2(3x) = 1 − 6x
So, f o (g o h)(x) = f (1 − 6x) = 2(1 − 6x )
+ 3= 5 − 12x ………(2)
From (1) and (2), we
get (f o g) o h = f o (g o h)
Example 1.25
Find x if gff(x)
= fgg(x), given f (x) = 3x + 1 and g(x)
= x + 3 .
Solution
gff(x) = g [f
{f (x)}] (This means “g of f of f of x”)
= g [ f (3x
+1)] = g [ 3(3x +1)+1] = g (9x + 4)
g (9x + 4) = [ (9x
+ 4) + 3] = 9x + 7
fgg(x) = f [g
{g (x)}] (This means “f of g of g of x”)
= f [ g (x
+ 3)] = f [ (x + 3) + 3] = f (x + 6)
f (x + 6) = [ 3(x
+ 6) + 1 ] = 3x + 19
These two quantities
being equal, we get 9x + 7 = 3x + 19. Solving this equation we
obtain x = 2.
Related Topics