Cartesian Product of three Set

Cartesian Product of three Set

If A, B, C are three non-empty sets then the cartesian product of three sets is the set of all possible ordered triplets given by

A× B ×C= {(a,b,c) for all a ∈ A,b ∈ B,c ∈ C }

Illustration for Geometrical understanding of cartesian product of two and three sets

Let A = {0,1}, B = {0,1}, C  = {0,1}

A×B  = {0,1}×{0,1} = {(0, 0),(0,1),(1, 0),(1,1)}

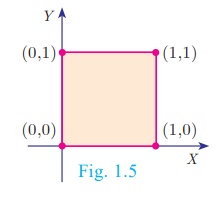
Representing A×B  in the xy - plane we get a picture shown in Fig. 1.5.

(A×B)×C= {(0, 0),(0,1),(1, 0),(1,1)} ×{0,1}

= {(0, 0, 0),(0, 0,1),(0,1, 0),(0,1,1),(1, 0, 0),(1, 0,1)(1,1, 0),(1,1,1)}

 Representing A×B ×C  in the xyz - plane we get a picture as shown in Fig. 1.6

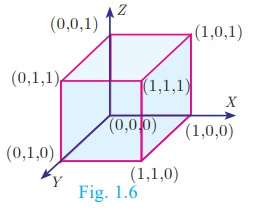
Thus, A×B  represent vertices of a square in two dimensions and A×B ×C  represent vertices of a cube in three dimensions.

NOTES

 In general, cartesian product of two non-empty sets provides a shape in two dimensions and cartesian product of three non-empty sets provide an object in three dimensions.