Two dimensional viewing

Two dimensional viewing

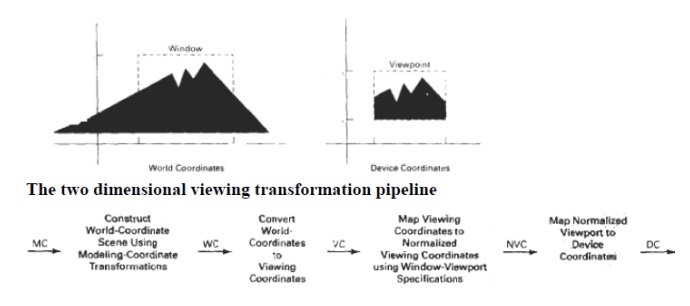
Two dimensional viewing The viewing pipeline A world coordinate area selected for display is called a window. An area on a display device to which a window is mapped is called a view port. The window defines what is to be viewed the view port defines where it is to be displayed. The mapping of a part of a world coordinate scene to device coordinate is referred to as viewing transformation. The two d imensional viewing transformation is referred to as window to view port transformation of windowing transformation.

A viewing transformation using standard rectangles for the window and viewport

The viewing transformation in several steps, as indicated in Fig. First, we construct the scene in world coordinates using the output primitives. Next to obtain a particular orientation for the window, we can set up a two-dimensional viewing-coordinate system in the world coordinate plane, and define a window in the viewing-coordinate system. The viewing- coordinate reference frame is used to provide a method for setting up arbitrary orientations for rectangular windows.

Once the viewing reference frame is established, we can transform descriptions in world coordinates to viewing coordinates. We then define a viewport in normalized coordinates (in the range from 0 to 1) and map the viewing-coordinate description of the scene to normalized coordinates.

At the final step all parts of the picture that lie outside the viewport are clipped, and the contents of the viewport are transferred to device coordinates. By changing the position of the viewport, we can view objects at different positions on the display area of an output device.

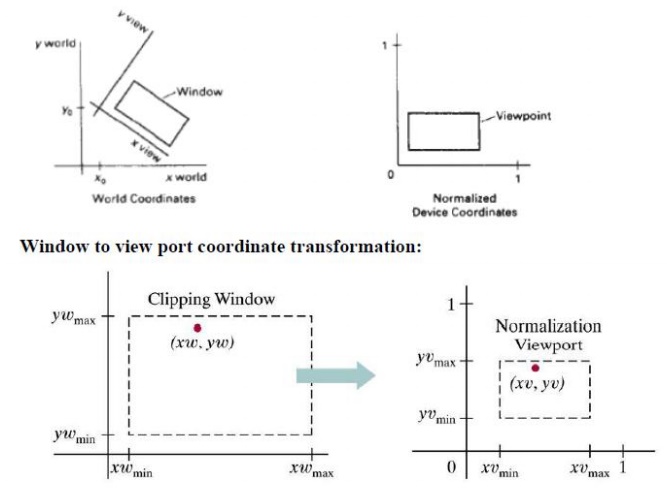
A point at position (xw,yw) in a designated window is mapped to viewport coordinates (xv,yv) so that relative positions in the two areas are the same. The figure illustrates the window to view port mapping. A point at position (xw,yw) in the window is mapped into position (xv,yv) in the associated view port. To maintain the same relative placement in view port as in window The conversion is performed with the following sequence of transformations.

1.  Perform a scaling transformation using point position of (xw min, yw min) that scales the window area to the size of view port.

2. Translate the scaled window area to the position of view port. Relative proportions of objects are maintained if scaling factor are the same(Sx=Sy).

Otherwise world objects will be stretched or contracted in either the x or y direction when displayed on output device. For normalized coordinates, object descriptions are mapped to various display devices. Any number of output devices can be open in particular application and another window view port transformation can be performed for each open output device. This mapping called the work station transformation is accomplished by selecting a window area in normalized apace and a view port are in coordinates of display device.

Mapping selected parts of a scene in normalized coordinate to different video monitors with work station transformation.

Window to Viewport transformation

The window defined in world coordinates is first transformed into the normalized device coordinates. The normalized window is then transformed into the viewport coordinate. The window to viewport coordinate transformation is known as workstation transformation. It is achieved by the following steps

1. The object together with its window is translated until the lower left corner of the window is at the orgin.

2. Object and window are scaled until the window has the dimensions of the viewport

3. Translate the viewport to its correct position on the screen.

The relation of the window and viewport display is expressed as XV-XVmin XW-XWmin

-------------- = ----------------

XVmax-XVmin XWmax-XWmin

YV-Yvmin YW-YWmin

-------------- = ----------------

YVmax-YVmin YWmax-YWmin

XV=XVmin + (XW-XWwmin)Sx

YV=YVmin + (YW-YWmin)Sy

XVmax-XVmin

Sx= --------------------

XWmax-Xwmin

YVmax-YVmin

Sy= --------------------

YWmax-YWmin

2D Clipping

The procedure that identifies the portion of a picture that are either inside or outside of a specified regin of space is referred to as clipping. The regin against which an object is to be clipped is called a clip window or clipping window.

The clipping algorithm determines which points, lines or portions of lines lie within the clipping window. These points, lines or portions of lines are retained for display. All other are discarded. Possible clipping are

1. Point clipping

2. Line clipping

3. Area clipping

4. Curve Clipping

5. Text Clipping

Point Clipping:

The points are said to be interior to the clipping if XWmin <= X <=XW max

YWmin <= Y <=YW max

The equal sign indicates that points on the window boundary are included within the window.

Line Clipping:

-   The lines are said to be interior to the clipping window, if the two end points of the lines are interior to the window.

-   If the lines are completely right of, completely to the left of, completely above, or completely below the window, then it is discarded.

-   Both end points of the line are exterior to the window, then the line is partially inside and partially outside the window.The lines which across one or more clipping boundaries requires calculation of multiple intersection points to decide the visible portion of them.To minimize the intersection calculation and increase the efficiency of the clipping algorithm, initially completely visible and invisible lines are identified and then intersection points are calculated for remaining lines.

There are many clipping algorithms. They are

1.Sutherland and cohen subdivision line clipping algorithm

It is developed by Dan Cohen and Ivan Sutharland. To speed up the processing this algorithm performs initial tests that reduces the number of intersections that must be calculated.

given a line segment, repeatedly:

1.     check for trival acceptance both

2. check for trivial rejection

both endpoints of the same side of clip rectangle 3. both endpoints outside clip rectangle

Divide segment in two where one part can be trivially rejected

Clip rectangle extended into a plane divided into 9 regions . Each region is defined by a unique 4-bit string

·        left bit = 1: above top edge (Y > Ymax)

·        2nd bit = 1: below bottom edge (Y < Ymin)

·        3rd bit = 1: right of right edge (X > Xmax)

·        right bit = 1: left of left edge (X < Xmin)

·        left bit = sign bit of (Ymax - Y)

·        2nd bit = sign bit of (Y - Ymin)

·        3rd bit = sign bit of (Xmax - X)

·        right bit = sign bit of (X - Xmin)

(The sign bit being the most significant bit in the binary representation of the value. This bit is '1' if the number is negative, and '0' if the number is positive.)

The frame buffer itself, in the center, has code 0000. 1001 | 1000 | 1010

-------------------------

0001 | 0000 | 0010

-------------------------

0101 | 0100 | 0110 For each line segment:

1. each end point is given the 4-bit code of its region

2. repeat until acceptance or rejection

1. if both codes are 0000 -> trivial acceptance

2. if logical AND of codes is not 0000 -> trivial rejection

3. divide line into 2 segments using edge of clip rectangle

1. find an endpoint with code not equal to 0000

2. lines that cannot be identified as completely inside or outside are checked for the intersection with two boundaries.

3. break the line segment into 2 line segments at the crossed edge

4. forget about the new line segment lying completely outside the clip rectangle

5. draw the line segment which lies within the boundary regin.

2. Mid point subdivision algorithm

If the line partially visible then it is subdivided in two equal parts. The visibility tests are then applied to each half. This subdivision process is repeated until we get completely visible and completely invisible line segments.

Mid point sub division algorithm

1. Read two end points of the line P1(x1,x2), P2(x2,y2)

2. Read two corners (left top and right bottom) of the window, say (Wx1,Wy1 and Wx2, Wy2)

3. Assign region codes for two end points using following steps

Initialize code with bits 0000 Set Bit 1 – if ( x < Wx1 ) Set Bit 2 – if ( x > Wx1 ) Set Bit 3 – if ( y < Wy1)

Set Bit 4 – if ( y > Wy2)

4. Check for visibility of line

a. If region codes for both endpoints are zero then the line is completely visible. Hence draw the line and go to step 6.

b. If the region codes for endpoints are not zero and the logical ANDing of them is also nonzero then the line is completely invisible, so reject the line and go to step6

c.  If region codes for two end points do not satisfy the condition in 4a and 4b the line is partially visible.

5. Divide the partially visible line segments in equal parts and repeat steps 3 through 5 for both subdivided line segments until you get completely visible and completely invisible line segments.

6. Stop.

This algorithm requires repeated subdivision of line segments and hence many times it is slower than using direct calculation of the intersection of the line with the clipping window edge.

3. Liang-Barsky line clipping algorithm

The cohen Sutherland clip algorithm requires the large no of intesection calculations.here this is reduced. The update parameter requires only one division and windows intersection lines are computed only once.

The parameter equations are given as

X=x1+u                   x, Y=Y1 + u     y

0<=u<=1, where                 x =x2-x1 , u    y=y2-y1

Algorithm

1. Read the two end points of the line p1(x,y),p2(x2,y2)

2. Read the corners of the window (xwmin,ywmax), (xwmax,ywmin)

3. Calculate the values of the parameter p1,p2,p3,p4 and q1,q2,q3,q4m such that

4. p1=  x q1=x1-xwmin

p2= - x q2=xwmax-x1 p3=  y q3=y1-ywmin p4= - y q4=ywmax-y1

5. If pi=0 then that line is parallel to the ith boundary. if qi<0 then the line is completely outside the boundary. So discard the linesegment and and goto stop.

Else

{

Check whether the line is horizontal or vertical and check the line endpoint with the corresponding boundaries. If it is within the boundary area then use them to draw a line. Otherwise use boundary coordinate to draw a line. Goto stop.

}

6. initialize values for U1 and U2 as U1=0,U2=1

7. Calculate the values forU= qi/pi for I=1,2,3,4

8. Select values of qi/pi where pi<0 and assign maximum out of them as u1

9. If (U1<U2)

{

Calculate the endpoints of the clipped line as follows XX1=X1+u1  x

XX2=X1+u 2 x YY1=Y1+u1  y YY2=Y1+u 2 y

}

10.Stop.

4. Nicholl-lee Nicholl line clipping

It Creates more regions around the clip window. It avoids multiple clipping of an individual line segment. Compare with the previous algorithms it perform few comparisons and divisions . It is applied only 2 dimensional clipping. The previous algorithms can be extended to 3 dimensional clipping.

1.     For the line with two end points p1,p2 determine the positions of a point for 9 regions. Only three regions need to be considered (left,within boundary, left upper corner).

2.  If p1 appears any other regions except this, move that point into this region using some reflection method.

3. Now determine the position of p2 relative to p1. To do this depends on p1 creates some new region.

a. If both points are inside the region save both points.

b. If p1 inside , p2 outside setup 4 regions. Intersection of appropriate boundary is calculated depends on the position of p2.

c. If p1 is left of the window, setup 4 regions . L, Lt,Lb,Lr

1. If p2 is in region L, clip the line at the left boundary and save this intersection to p2.

2. If p2 is in region Lt, save the left boundary and save the top boundary.

3. If not any of the 4 regions clip the entire line.

d. If p1 is left above the clip window, setup 4 regions . T, Tr,Lr,Lb 1. If p2 inside the region save point.

2. else determine a unique clip window edge for the intersection calculation.

e. To determine the region of p2 compare the slope of the line to the slope of the boundaries of the clip regions.

Line clipping using non rectangular clip window

Circles and other curved boundaries clipped regions are possible, but less commonly used. Clipping algorithm for those curve are slower.

1. Lines clipped against the bounding rectangle of the curved clipping region. Lines outside the region is completely discarded.

2. End points of the line with circle center distance is calculated . If the squre of the 2 points less than or equal to the radious then save the line else calculate the intersection point of the line.

Polygon clipping

Splitting the concave polygon

It uses the vector method , that calculate the edge vector cross products in a counter clock wise order and note the sign of the z component of the cross products. If any z component turns out to be negative, the polygon is concave and we can split it along the line of the first edge vector in the cross product pair.

Sutherland – Hodgeman polygon Clipping Algorithm

1. Read the coordinates of all vertices of the polygon.

2. Read the coordinates of the clipping window.

3. Consider the left edge of the window.

4. Compare the vertices of each edge of the polygon, Individually with the clipping plane.

5.  Save the resulting intersections and vertices in the new list of vertices according to four possible relationships between the edge and the clipping boundary discussed earlier.

6. Repeats the steps 4 and 5 for remaining edges of the clipping window. Each time the resultant vertices is successively passed the next edge of the clipping window.

7. Stop.

The Sutherland –Hodgeman polygon clipping algorithm clips convex polygons correctly, But in case of concave polygons clipped polygon may be displayed with extraneous lines. It can be solved by separating concave polygon into two or more convex polygons and processing each convex polygons separately.

The following example illustrates a simple case of polygon clipping.

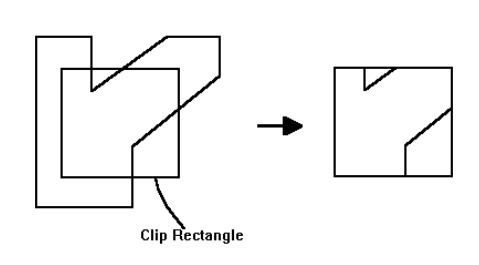
WEILER –Atherton Algorithm

Instead of proceding around the polygon edges as vertices are processed, we sometime wants to follow the window boundaries.For clockwise processing of polygon vertices, we use the following rules.

-  For an outside to inside pair of vertices, follow the polygon boundary.

-  For an inside to outside pair of vertices, follow a window boundary in a clockwise direction.

Curve Clipping

It involves non linear equations. The boundary rectangle is used to test for overlap with a rectangular clipwindow. If the boundary rectangle for the object is completely inside the window , then save the object (or) discard the object.If it fails we can use the coordinate extends of individual quadrants and then octants for preliminary testing before calculating curve window intersection.

Text Clipping

The simplest method for processing character strings relative to a window boundary is to use the all or none string clipping strategy. If all the string is inside then accept it else omit it.

We discard only those character that are not completely inside the window. Here the boundary limits of individual characters are compared to the window.

Exterior clipping

The picture part to be saved are those that are outside the region. This is referred to as exterior clipping. An application of exterior clipping is in multiple window systems.

Objects within a window are clipped to the interior of that window. When other higher priority windows overlap these objects , the ojects are also clipped to the exterior of the overlapping window.