Animation

Animation

Computer animation refers to any time sequence of visual changes in a scene.

Computer animations can also be generated by changing camera parameters such as position, orientation and focal length.

Applications of computer-generated animation are entertainment, advertising, training and education.

Example : Advertising animations often transition one object shape into another.

Frame-by-Frame animation

Each frame of the scene is separately generated and stored. Later, the frames can be recoded on film or they can be consecutively displayed in "real-time playback" mode

Design of Animation Sequences

An animation sequence in designed with the following steps: o Story board layout

o  Object definitions

·       Key-frame specifications

Story Board:

Generation of in-between frames.

The story board is an outline of the action.

It defines the motion sequences as a set of basic events that are to take place.

Depending on the type of animation to be produced, the story board could consist of a set of rough sketches or a list of the basic ideas for the motion.

Object Definition

An object definition is given for each participant in the action.

Objects can be defined in terms of basic shapes such as polygons or splines.

The associated movements of each object are specified along with the shape.

Key frame

A key frame is detailed drawing of the scene at a certain time in the animation sequence.

Within each key frame, each object is positioned according to the time for that frame.

Some key frames are chosen at extreme positions in the action; others are spaced so that the time interval between key frames is not too much.

In-betweens

In betweens are the intermediate frames between the key frames.

The number of in between needed is determined by the media to be used to display the animation.

Film requires 24 frames per second and graphics terminals are refreshed at the rate of 30 to 60 frames per seconds.

Time intervals for the motion are setup so there are from 3 to 5 in-between for each

pair of key frames.

Depending on the speed of the motion, some key frames can be duplicated. For a 1 min film sequence with no duplication, 1440 frames are needed.

Other required tasks are

Motion verification

Editing

Production and synchronization of a sound track.

General Computer Animation Functions

Steps in the development of an animation sequence are,

Object manipulation and rendering

Camera motion

Generation of in-betweens

Animation packages such as wave front provide special functions for designing the animation and processing individuals objects.

Animation packages facilitate to store and manage the object database.

Object shapes and associated parameter are stored and updated in the database.

Motion can be generated according to specified constraints using 2D and 3D transformations.

Standard functions can be applied to identify visible surfaces and apply the rendering algorithms.

Camera movement functions such as zooming, panning and tilting are used for motion simulation.

Given the specification for the key frames, the in-betweens can be automatically generated.

Raster Animations

On raster systems, real-time animation in limited applications can be generated using raster operations.

Sequence of raster operations can be executed to produce real time animation of either 2D or 3D objects.

We can animate objects along 2D motion paths using the color-table transformations.

Predefine the object as successive positions along the motion path, set the successive blocks of pixel values to color table entries.

Set the pixels at the first position of the object to „on‟ values, and set the pixels at the other object positions to the background color.

The animation is accomplished by changing the color table values so that the object is „on‟ at successive positions along the animation path as the preceding position is set to the background intensity.

Computer Animation Languages

Animation functions include a graphics editor, a key frame generator and standard graphics routines.

The graphics editor allows designing and modifying object shapes, using spline surfaces, constructive solid geometry methods or other representation schemes.

Scene description includes the positioning of objects and light sources defining the photometric parameters and setting the camera parameters.

Action specification involves the layout of motion paths for the objects and camera.

Keyframe systems are specialized animation languages designed dimply to generate the in-betweens from the user specified keyframes.

Parameterized systems allow object motion characteristics to be specified as part of the object definitions. The adjustable parameters control such object characteristics as degrees of freedom motion limitations and allowable shape changes.

Scripting systems allow object specifications and animation sequences to be defined with a user input script. From the script, a library of various objects and motions can be constructed.

Keyframe Systems

Each set of in-betweens are generated from the specification of two keyframes.

For complex scenes, we can separate the frames into individual components or objects called cells, an acronym from cartoon animation.

Morphing

Transformation of object shapes from one form to another is called Morphing.

Morphing methods can be applied to any motion or transition involving a change in shape. The example is shown in the below figure.

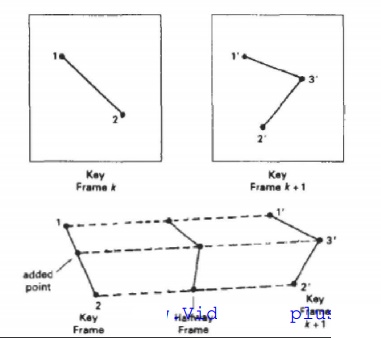
Suppose we equalize the edge count and parameters L_k and L_k+1 denote the number of line segments in two consecutive frames. We define,

L_max = max (L_k, L_k+1)

L_min = min(L_k , L_k+1)

Ne = Lmax mod Lmin

N_s = int (L_max/L_min)

The preprocessing is accomplished by

^§    Dividing N_e edges of keyframe_min into N_s+1 section.

^§    Dividing the remaining lines of keyframe_min into N_s sections.

For example, if L_k = 15 and L_k+1 = 11, we divide 4 lines of keyframe_k+1 into 2 sections each. The remaining lines of keyframe_k+1 are left infact.

If the vector counts in equalized parameters V_k and V_k+1 are used to denote the number of vertices in the two consecutive frames. In this case we define

V_max = max(V_k,V_k+1), V_min = min( V_k,V_k+1) and

N_ls = (V_max -1) mod (V_min – 1)

N_p  = int ((V_max – 1)/(V_min – 1 ))

Preprocessing using vertex count is performed by

^§    Adding N_p points to N_ls line section of keyframe_min.

^§    Adding N_p-1 points to the remaining edges of keyframe_min.

Simulating Accelerations

Curve-fitting techniques are often used to specify the animation paths between key frames. Given the vertex positions at the key frames, we can fit the positions with linear or nonlinear paths. Figure illustrates a nonlinear fit of key-frame positions. This determines the trajectories for the in-betweens. To simulate accelerations, we can adjust the time spacing for the in-betweens.

For constant speed (zero acceleration), we use equal-interval time spacing for the in-betweens. Suppose we want n in-betweens for key frames at times t1 and t2.

The time interval between key frames is then divided into n + 1 subintervals, yielding an in-between spacing of

∆= t2-t1/n+1

we can calculate the time for any in-between as

tBj = t1+j ∆t, j = 1,2, . . . . . . n

Motion Specification

These are several ways in which the motions of objects can be specified in an animation system.

Direct Motion Specification

Here the rotation angles and translation vectors are explicitly given.

Then the geometric transformation matrices are applied to transform coordinate positions.

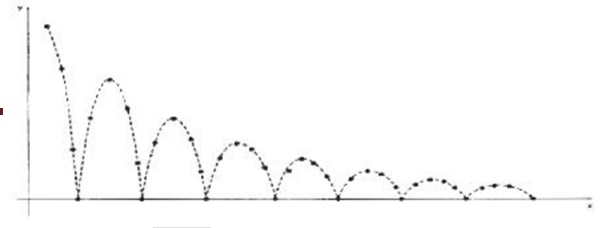
We can approximate the path of a bouncing ball with a damped, rectified, sine curve

y (x) = A / sin(ω_x + θ₀) /e^-kx

where A is the initial amplitude, ω is the angular frequency, θ₀ is the phase angle and k is the damping constant.