Chapter: Computer Graphics and Multimedia
Two Dimensional Graphics Transformations
TWO DIMENSIONAL GRAPHICS
TRANSFORMATIONS
Geometric Transformations
Changes in size, shape are accomplished with geometric transformation. It alter the coordinate descriptions of object.
The basic transformations are Translation, Roatation, Scaling. Other transformations are Reflection and shear.Basic transformations used to reposition and resize the two dimentional objects.
Two Dimensional Transformations
Translation
A
Translation is applied to an object by repositioning it along a straight line
path from one co-ordinate location to another. We translate a two dimensional
point by adding translation distances tx and ty to the original position (x,y)
to move the point to a new location (x’,y’)
X’=x+tx
Y’=y+ty
triangle = { p1=(1,0), p2=(2,0), p3=(1.5,2) }
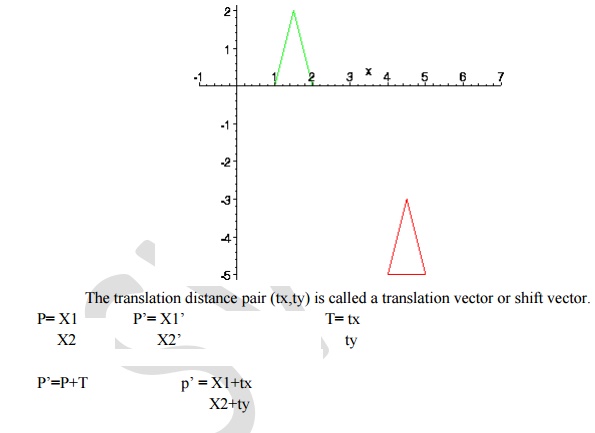
It moves
objects without deformation. (ie) Every point on the objet is translated by the
same amount. It can be applied to lines, polygons.
Rotation
A two
dimensional rotation is applied to an object by repositioning it along a
circular path in the xy plane. To generate a rotation, we specify a rotation
angle theta and the position (xr,yr) of the rotation point ( or pivot point)
about which the object is to be rotated.
Positive
value of the rotation angle defines counter clock wise rotation. Negative value
of the rotation angle defines the clock wise rotation.
X’=xcosθ – y sinθ
Y’=xsinθ + y cosθ
Using
column vector P’=P*R R= Cosθ -Sinθ
Sinθ Cosθ
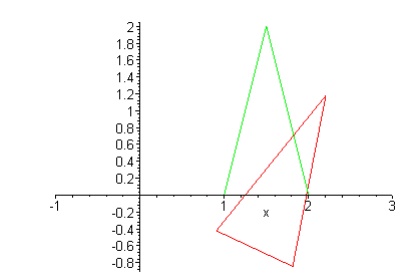
Rotation of an arbitary pivot point
Rotation
of a point about any specified rotation position (xr,yr)
X’= Xr +(X-Xr)Cosθ –(Y-Yr)Sinθ
Y’=Yr+(X-Xr)Sinθ +(Y-Yr)Cosθ
It moves
objects without deformations. Every point on an object is rotated through the
same angle.
Scaling
A scaling
transformation alters the size of an object. This operation can be carried out
for polygon by multiplying the coordinate values (x,y) of each vertex by
scaling factors sx and sy to produce the transformed coordinates (x’,y’).
X’=x.sx
Y’=y.sy
P= X1 P’=
X1’ S= sx 0
X2 X2’ 0 sy
P’=P*S
If sx=sy
, then it produces the uniform scaling
Sx<>
sy , different scaling.
If
sx,sy<0, then it produces the reduced object size
If sx,sy
> 0, then it produces the enlarged size objects.
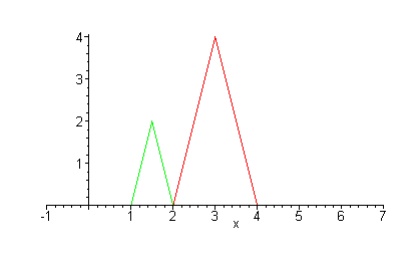
By
choosing the position called fixed point, we can control the location of the
scaled object. This point is remain unchanged after the scaling transformation.
X’= Xf +(X-Xf)sx => X’= X.sx
+(Xf(1-sx))
Y’=Yf+(Y-Yf)sy => Y’= Y.sy
+Yf(1-sy)
Matrix representations and homogeneous coordinates
Graphics
applications involves sequences of geometric transformations. The basic
transformations expressed in terms of
P’=M1 *P
+M2
P, P’ à Column vectors.
M1 à 2 x 2 array containing multiplicative factors
M2 à 2 Element column matrix containing translation
terms
For
translation à M1 is
the identity matrix
For
rotation or scaling àM2
contains transnational terms associated with the pivot point or scaling fixed
point.
For
coordinate positions are scaled, then rotated then translated, these steps are
combined together into one step, final coordinate positions are obtained
directly from the initial coordinate values.
To do
this expand the 2 x 2 matrix into 3 x 3 matrix.
To
express 2 dimensional transformation as a multiplication, we represent each
cartesion coordinate position (x,y) with the homogeneous co ordinate triple
(Xh,Yh, h) where
X= xh/h,
Y=Yh/h
So we can
write (h.x, h.y,h), set h=1. Each two dimensional position is represented with
homogeneous coordinates(x,y,1). Coordinates are represented with three element
column vector. Transformation operations are written as 3 by 3 matrices.
For
translation

P’=T(tx,ty)*P
Inverse
of the translation matrix is obtained by replacing tx, ty by –tx, -ty
Similarly
rotation about the origin
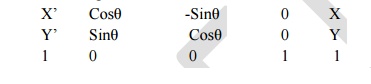
P’=
R(θ)*P
We get
the inverse rotation matrix when θ is replaced with (-θ)
Similarly
scaling about the origin
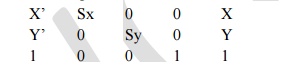
Composite
transformations
Sequence
of transformations is called as composite transformation. It is obtained by
forming products of transformation matrices is referred as a concatenation (or)
composition of matrices.
Translation:
-
Two
successive translations
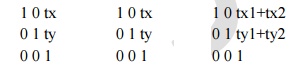
T(tx1,ty1)
+ T(tx2,ty2) = T(tx1+tx2, ty1+ty2)
Two
successive translations are additive.
Rotation
Two
successive rotations are additive.
R(θ1)*
R(θ2)= R(θ1+ θ2)
P’=P.
R(θ1+ θ2)
Scaling

S(x1,y1).S(x2,y2)
= S(sx1.sx2 , sy1.sy2)
1. the order
we perform multiple transforms can matter
·
eg. translate + scale can differ from scale +
translate
·
eg. rotate + translate can differ from translate +
rotate
·
eg. rotate + scale can differ from scale + rotate
(when scale_x differs from scale_y)
2. When does
M1 + M2 = M2 + M1?

General pivot point rotation
Rotation
about any selected pivot point (xr,yr) by performing the following sequence of translate
– rotate
– translate operations.
1. Translate
the object so that the pivot point is at the co-ordinate origin.
2. Rotate
the object about the coordinate origin
3. Translate
the object so that the pivot point is returned to its original position
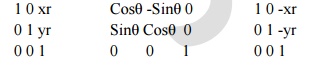
Concatenation properties
T(xr,yr).R(θ).T(-xr,-yr)
= R(xr,yr, θ)
Matrix
multiplication is associative. Transformation products may not be commutative.
Combination
of translations, roatations, and scaling can be expressed as
X’ rSxx rSxy trSx X
Y’ rSyx rSyy trSy Y
1 0 0 1 1
Other transformations
Besides
basic transformations other transformations are reflection and shearing
Reflection :
Reflection
is a transformation that produces the mirror image of an object relative to an
axis of reflection. The mirror image is generated relative to an axis of
reflection by rotating the object by 180 degree about the axis.
Reflection
about the line y=0 (ie about the x axis), the x-axis is accomplished with the
transformation matrix.
1 0 0
0 -1 0
0 0 1
It keeps
the x values same and flips the y values of the coordinate positions.
Reflection about the y-axis
-1 0 0 0
1 0 0 0 1
It keeps
the y values same and flips the x values of the coordinate positions.
Reflection relative to the coordinate origin.
-1 0 0 0
-1 0 0 0 1
Reflection
relative to the diagonal line y=x , the matrix is 0 1 0 1 0 0 0 0 1
Reflection
relative to the diagonal line y=x , the matrix is 0 -1 0 -1 0 0 0 0 1
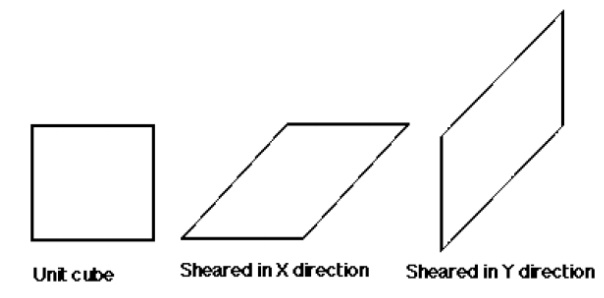
Shear
A
transformation that alter the shape of an object is called the shear
transformation. Two shearing transformations
1. Shift x
coordinate values ( X- shear)
2. Shifts y
coordinate values. (Y-shear)
In both
cases only one coordinate ( x or y ) changes its coordinates and other
preserves its values.
X –Shear
It
preserves the y value and changes the x value which causes vertical lines to
tilt right or left
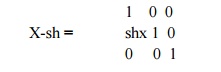
X’=
X+shx*y
Y’=Y
Y –Shear
It
preserves the x value and changes the y value which causes vertical lines to
tilt right or left 1 shy 0
Y-sh = 0
1 0 0 0 1
Y’=
Y+shy*X
X’=X
Shearing Relative to other
reference line
We can
apply x and y shear transformations relative to other reference lines. In x shear
transformation we can use y reference line and in y shear we can use x
reference line.
The
transformation matrices for both are given below.

which
generates transformed coordinate positions. x’=x , y’= shy(x-xref)+y
This transformation
shifts a coordinate position vertically by an amount proposal to its distance
from the reference line x=x ref.
Transformations between
coordinate systems
Transformations between Cartesian coordinate
systems are achieved with a sequence of translate-rotate transformations. One
way to specify a new coordinate reference frame is to give the position of the
new coordinate origin and the direction of the new y-axis. The direction of the
new x-axis is then obtained by rotating the y direction vector 90 degree
clockwise. The transformation matrix can be calculated as the concatenation of
the translation that moves the new origin to the old co-ordinate origin and a
rotation to align the two sets of axes. The rotation matrix is obtained from
unit vectors in the x and y directions for the new system
Related Topics