3D Transformation

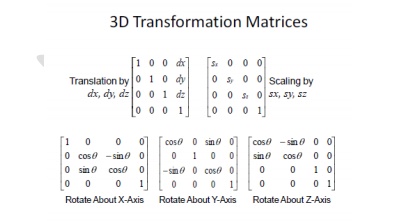
3D Transformation

3-D Coordinate Spaces

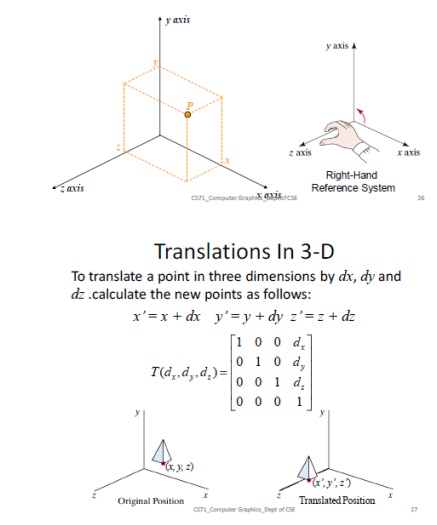
Rotations In 3-D When we performed rotations in two dimensions we only had the choice of rotating about the z axis In the case of three dimensions we have more options – Rotate about x – Rotate about y – Rotate about z

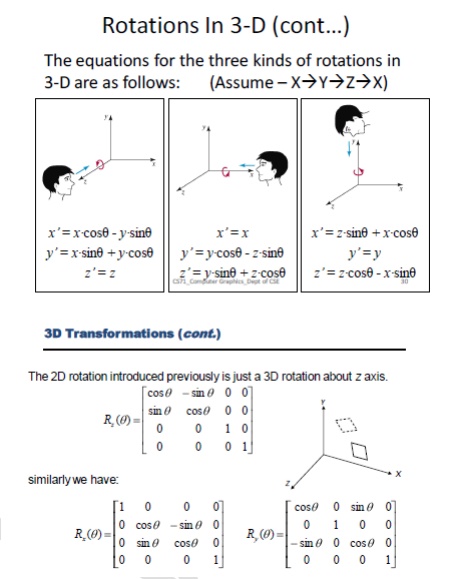
General 3D Rotations • Rotation about an axis that is parallel to one of the coordinate axes : 1. Translate the object so that the rotation axis coincides with the parallel coordinate axis 2. Perform the specified rotation about the axis 3. Translate the object so that the rotation axis is moved back to its original position • Not parallel : 1. Translate the object so that the rotation axis passes through the coordinate origin 2. Rotate the object so that the axis of rotation coincides with one of the coordinate axes 3. Perform the specified rotation about the axis 4. Apply inverse rotations to bring the rotation axis back to its original orientation 5. Apply the inverse translation to bring back the rotation axis to its original position

3 D Transformation functions • Functions are – translate3(translateVector, matrixTranslate) – rotateX(thetaX, xMatrixRotate) – rotateY(thetaY, yMatrixRotate) – rotateZ(thetaZ, zMatrixRotate) – scale3(scaleVector,matrixScale) • To apply transformation matrix to the specified points , – transformPoint3(inPoint, matrix,outPoint) • We can construct composite transformations with the following functions – composeMatrix3 – buildTransformationMatrix3 – composeTransformationMatrix3 CS71_Computer Graphics_Dept of CSE 34 Reflections In 3-D • Three Dimensional Reflections can be performed relative to a selected reflection axis or a selected reflection plane • Consider a reflection that converts coordinate specifications from a right handed system to left handed system. • This transformation changes the sign of Z coordinate leaving x and y coordinates

Shears In 3-D

Shearing transformations are used to distortions in the shape of an object. In 2D, shearing is applied to x or y axes. In 3D it can applied to z axis also

The following transformation produces an Z axis shear

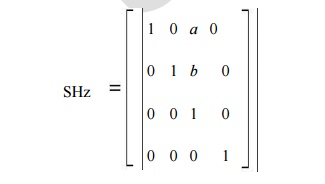
Parameters a and b can be assigned any real values