Mathematics - Trigonometric functions and their properties | 11th Mathematics : UNIT 3 : Trigonometry
Chapter: 11th Mathematics : UNIT 3 : Trigonometry
Trigonometric functions and their properties
The trigonometric ratios to any angle in terms of radian measure are called trigonometric functions.
Trigonometric functions and their properties
We have studied the principles of trigonometric ratios in the lower classes using acute angles . But we come across many angles which are not acute. We shall extend the acute angle idea and define trigonometric functions for any angle. The trigonometric ratios to any angle in terms of radian measure are called trigonometric functions.
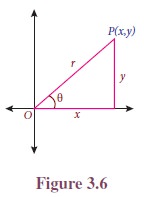
Let P(x, y) be a point other than the origin on the terminal side of an angle ╬Ė in standard position . Let OP = r.
Thus, r = ŌłÜ(x2 + y2)
The six trigonometric functions of ╬Ė are defined as follows:

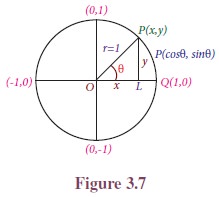
Consider the unit circle x2 +y2 = 1. Let P(x, y) be a point on the unit circle where the terminal side of the angle ╬Ė intersects the unit circle.
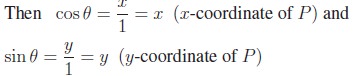
Thus, the coordinates of any point P(x, y) on the unit circle is (cos ╬Ė,sin ╬Ė). In this way, the angle measure ╬Ė is associated with a point on the unit circle.
The following table illustrates how trigonometric function values are determined for a Quadrantal angles using the above explanation.


Consider a unit circle with the centre at the origin. Let the angle zero (in radian measure) be associated with the point A(1, 0) on the unit circle. Draw a tangent to the unit circle at the point A(1, 0). Let t be a real number such that t is y- coordinate of a point on the tangent line.

For each real number t, identify a point B(x, y) on the unit circle such that the arc length AB is equal to t. If t is positive, choose the point B(x, y) in the anticlockwise direction, otherwise choose it in the clockwise direction. Let ╬Ė be the angle subtended by the arc AB at the centre. In this way, we have a function w(t) associating a real number t to a point on the unit circle. Such a function is called a wrapping function . Then s = r╬Ė gives arc length t = ╬Ė.
Now, define sin t = sin ╬Ė and cos t = cos ╬Ė.
Clearly, sin t = sin ╬Ė = y and cos t = cos ╬Ė = x.
Using sin t and cos t, other trigonometric functions can be defined as functions of real numbers.

Signs of Trigonometric functions
Consider a unit circle with centre at the origin. Let ╬Ė be in standard position. Let P(x, y) be the point on the unit circle corresponding to the angle ╬Ė. Then, cos ╬Ė = x, sin ╬Ė = y and tan ╬Ė = y/x.
The values of x and y are positive or negative depending on the quadrant in which P lies.
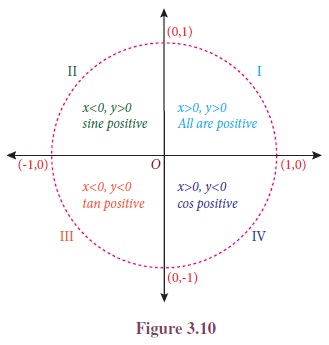
In the first quadrant:
cos ╬Ė = x > 0 (positive); sin ╬Ė = y > 0 (positive)
Thus, cos ╬Ė and sin ╬Ė and hence all trigonometric functions are positive in the first quadrant.
In the second quadrant:
cos ╬Ė = x < 0 (negative); sin ╬Ė = y > 0 (positive)
Thus, sin ╬Ė and cosec ╬Ė are positive and others are negative.
Similarly, we can find the sign of trigonometric functions in other two quadrants.
Let us illustrate the above discussions in Figure 3.10.
 Signs of trigonometric functions in various quadrants can be remembered with the slogan
Signs of trigonometric functions in various quadrants can be remembered with the slogan
ŌĆ£All Students Take ChocolateŌĆØ. (ASTC rule)






We know that a function f is said to be a periodic function with period p, if there exists a smallest positive number p such thatf(x + p) = f(x) for all x in the domain.
For example, sin (x + 2nŽĆ) = sin x, n Ōłł Z.
i.e., sin (x + 2ŽĆ) = sin (x + 4ŽĆ) = sin (x + 6ŽĆ) = . . . = sin x Thus, sin x is a periodic function with period 2ŽĆ.
Similarly, cos x , cosecx and sec x are periodic functions with period 2ŽĆ.
But tan x and cot x are periodic functions with period ŽĆ.
The periodicity of sin x and cos x can be viewed best using their graphs.
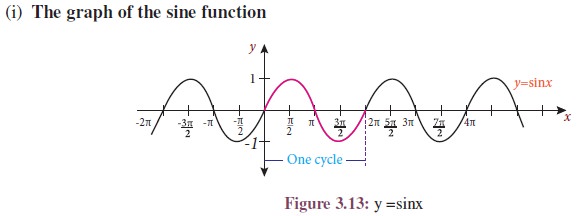
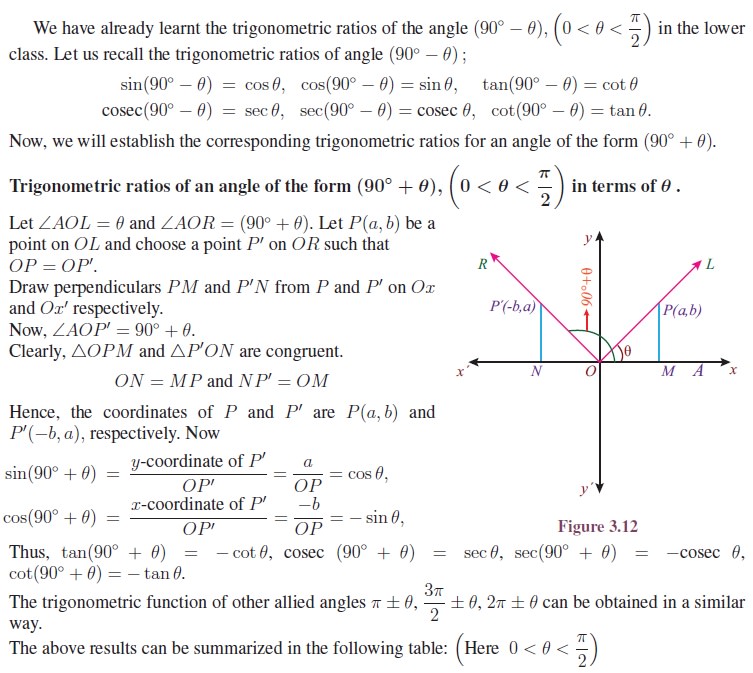
Here x represents a variable angle. Take the horizontal axis to be the x-axis and vertical axis to be the y-axis. Graph of the function y = sin x is shown in the Figure 3.13. First, note that it is periodic of period 2ŽĆ. Geometrically it means that if you take the curve and slide it 2ŽĆ either left or right, then the curve falls back on itself. Second, note that the graph is within one unit of the y-axis. The graph increases and decreases periodically. For instance, increases from ŌłÆŽĆ/2 to ŽĆ/2 and decreases from ŽĆ/2 to 3ŽĆ/2.

Basic trigonometric functions are examples of non-polynomial even and odd functions
Because cos(ŌłÆx) = cos x and sin(ŌłÆx) = ŌłÆ sin x for all x, it follows that cos x is an even function and sin x is an odd function.
Also note that sec x is an even function while tan x, cosec x and cot x are all odd functions. However, f(t) = t ŌłÆ cos t is neither even function nor odd function (why ?)


1. Trigonometric Functions of any angle in terms of Cartesian coordinates
We have studied the principles of trigonometric ratios in the lower classes using acute angles . But we come across many angles which are not acute. We shall extend the acute angle idea and define trigonometric functions for any angle. The trigonometric ratios to any angle in terms of radian measure are called trigonometric functions.

Let P(x, y) be a point other than the origin on the terminal side of an angle ╬Ė in standard position . Let OP = r.
Thus, r = ŌłÜ(x2 + y2)
The six trigonometric functions of ╬Ė are defined as follows:

Trigonometric ratios of Quadrantal angles
Let us recall that an angle in its standard position for which the terminal side coincides with one of the axes, is a Quadrantal angle. We shall find the trigonometric ratios for the quadrantal angles.
Consider the unit circle x2 +y2 = 1. Let P(x, y) be a point on the unit circle where the terminal side of the angle ╬Ė intersects the unit circle.
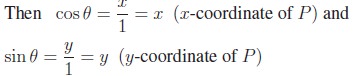
Thus, the coordinates of any point P(x, y) on the unit circle is (cos ╬Ė,sin ╬Ė). In this way, the angle measure ╬Ė is associated with a point on the unit circle.
The following table illustrates how trigonometric function values are determined for a Quadrantal angles using the above explanation.


2. Trigonometric Functions of real numbers
For applications of trigonometry to the problems in higher mathematics including calculus and to problems in physics and chemistry, scientists required trigonometric functions of real numbers. This was skillfully done by exhibiting a correspondence between an angle and an arc length denoting a real number on a unit circle.Consider a unit circle with the centre at the origin. Let the angle zero (in radian measure) be associated with the point A(1, 0) on the unit circle. Draw a tangent to the unit circle at the point A(1, 0). Let t be a real number such that t is y- coordinate of a point on the tangent line.

For each real number t, identify a point B(x, y) on the unit circle such that the arc length AB is equal to t. If t is positive, choose the point B(x, y) in the anticlockwise direction, otherwise choose it in the clockwise direction. Let ╬Ė be the angle subtended by the arc AB at the centre. In this way, we have a function w(t) associating a real number t to a point on the unit circle. Such a function is called a wrapping function . Then s = r╬Ė gives arc length t = ╬Ė.
Now, define sin t = sin ╬Ė and cos t = cos ╬Ė.
Clearly, sin t = sin ╬Ė = y and cos t = cos ╬Ė = x.
Using sin t and cos t, other trigonometric functions can be defined as functions of real numbers.

Signs of Trigonometric functions
Consider a unit circle with centre at the origin. Let ╬Ė be in standard position. Let P(x, y) be the point on the unit circle corresponding to the angle ╬Ė. Then, cos ╬Ė = x, sin ╬Ė = y and tan ╬Ė = y/x.
The values of x and y are positive or negative depending on the quadrant in which P lies.

In the first quadrant:
cos ╬Ė = x > 0 (positive); sin ╬Ė = y > 0 (positive)
Thus, cos ╬Ė and sin ╬Ė and hence all trigonometric functions are positive in the first quadrant.
In the second quadrant:
cos ╬Ė = x < 0 (negative); sin ╬Ė = y > 0 (positive)
Thus, sin ╬Ė and cosec ╬Ė are positive and others are negative.
Similarly, we can find the sign of trigonometric functions in other two quadrants.
Let us illustrate the above discussions in Figure 3.10.
ŌĆ£All Students Take ChocolateŌĆØ. (ASTC rule)

3. Allied Angles





4. Some Characteristics of Trigonometric Functions

Periodicity of Trigonometric Functions
We know that a function f is said to be a periodic function with period p, if there exists a smallest positive number p such thatf(x + p) = f(x) for all x in the domain.
For example, sin (x + 2nŽĆ) = sin x, n Ōłł Z.
i.e., sin (x + 2ŽĆ) = sin (x + 4ŽĆ) = sin (x + 6ŽĆ) = . . . = sin x Thus, sin x is a periodic function with period 2ŽĆ.
Similarly, cos x , cosecx and sec x are periodic functions with period 2ŽĆ.
But tan x and cot x are periodic functions with period ŽĆ.
The periodicity of sin x and cos x can be viewed best using their graphs.

Here x represents a variable angle. Take the horizontal axis to be the x-axis and vertical axis to be the y-axis. Graph of the function y = sin x is shown in the Figure 3.13. First, note that it is periodic of period 2ŽĆ. Geometrically it means that if you take the curve and slide it 2ŽĆ either left or right, then the curve falls back on itself. Second, note that the graph is within one unit of the y-axis. The graph increases and decreases periodically. For instance, increases from ŌłÆŽĆ/2 to ŽĆ/2 and decreases from ŽĆ/2 to 3ŽĆ/2.


Odd and Even trigonometric functions
Even and odd functions are functions satisfying certain symmetries. A real valued function f(x) is an even function if it satisfiesf(ŌłÆx) = f(x) for all real number x and an odd function if it satisfies f(ŌłÆx) = ŌłÆf(x) for all real number x.Basic trigonometric functions are examples of non-polynomial even and odd functions
Because cos(ŌłÆx) = cos x and sin(ŌłÆx) = ŌłÆ sin x for all x, it follows that cos x is an even function and sin x is an odd function.
Also note that sec x is an even function while tan x, cosec x and cot x are all odd functions. However, f(t) = t ŌłÆ cos t is neither even function nor odd function (why ?)


Tags : Mathematics , 11th Mathematics : UNIT 3 : Trigonometry
Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
11th Mathematics : UNIT 3 : Trigonometry : Trigonometric functions and their properties | Mathematics
Related Topics
11th Mathematics : UNIT 3 : Trigonometry