Application to Triangle

Application to Triangle

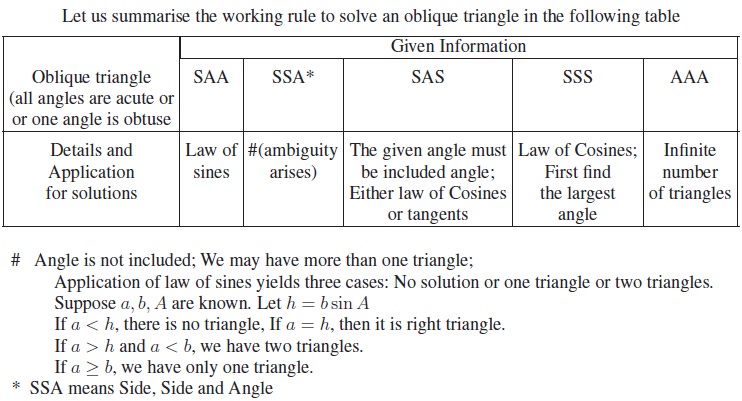
Much of architecture and engineering relies on triangular support on any structure where stability is desired. Trigonometry helps to calculate the correct angle for the triangular support. Also trigonometry envisages the builders to correctly layout a curved structure. For a right triangle, any two information with atleast one side say SS, SA are sufficient to find the remaining elements of the triangle. But, to find the solution of an oblique triangle we need three elements with atleast one side. If any three elements with atleast one side of a triangle are given, then the Law of Sines, the Law of Cosines, the Projection formula can be used to find the other three elements.

Working Rule:

·        In a right triangle, two sides determine the third side via the Pythagorean theorem and one acute angle determine the other by using the fact that acute angles in a right triangle are complementary.

·        If all the sides of a triangle are given, then we can use either cosine formula or half-angle formula to calculate all the angles of the triangle.

·        If any two angles and any one of the sides opposite to given angles are given, then we can use sine formula to calculate the other sides.

·        If any two sides of a triangle and the included angle are given, we cannot use the Law of sines; but then we can use the law of cosines to calculate other side and other angles of the triangle. In this case we have a unique triangle.

·        All methods of solving an oblique triangle require that the length of atleast one side must be provided.