Radian Measure

Radian Measure

Initially right triangles were used to define trigonometric ratios and angles were measured in degrees. But right triangles have limitations as they involve only acute angles. In degrees a full rotation corresponds to 360^◦ where the choice of 360 dates back thousands of years to the Babylonians. They might have chosen 360 based on the number of days in a year. But it does have the nice property of breaking into smaller angles like 30^◦, 45^◦, 60^◦, 90^◦ and 180^◦. In 17th century, trigonometry was extended to Physics and Chemistry where it required trigonometric functions whose domains were sets of real numbers rather than angles. This was accomplished by using correspondence between an angle and length of the arc on a unit circle. Such a measure of angle is termed as radian measure . For theoretical applications, the radian is the most common system of angle measurement. Radians are common unit of measurement in many technical fields, including calculus. The most important irrational number π plays a vital role in radian measures of angles. Let us introduce the radian measure of an angle.

 (i) All circles are similar. Thus, for a given central angle in any circle, the ratio of the intercepted arc length to the radius is always constant.

(ii) When s = r, we have an angle of 1 radian. Thus, one radian is the angle made at the centre of a circle by an arc with length equal to the radius of the circle.

(iii) Since the lengths s and r have same unit, θ is unitless and thus, we do not use any notation to denote radians.

(iv) θ = 1 radian measure, if s = r

θ = 2 radian measure, if s = 2r

Thus, in general θ = k radian measure, if s = kr.

Hence, radian measure of an angle tells us how many radius lengths, we need to sweep out along the circle to subtend the angle θ.

(v) Radian angle measurement can be related to the edge of the unit circle. In radian system, we measure an angle by measuring the distance travelled along the edge of the unit circle to where the terminal side of the angle intercepts the unit circle .

1. Relationship between Degree and Radian Measures

We have degree and radian units to measure angles. One measuring unit is better than another if it can be defined in a simpler and more intuitive way. For example, in measuring temperature, Celsius unit is better than Fahrenheit as Celsius was defined using 0^◦ and 100^◦ for freezing and boiling points of water. Radian measure is better for conversion and calculations. Radian measure is more convenient for analysis whereas degree measure of an angle is more convenient to communicate the concept between people. Greek Mathematicians observed the relation of π which arises from circumference of a circle and thus, π plays a crucial role in radian measure.

In unit circle, a full rotation corresponds to 360^â—¦ whereas, a full rotation is related to 2Ï€ radians, the circumference of the unit circle. Thus, we have the following relations:

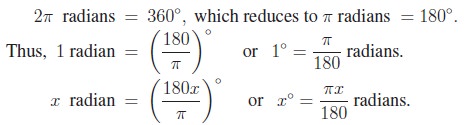
Observe that the scale used in radians is much smaller than the scale in degrees. The smaller scale makes the graphs of trigonometric functions more visible and usable. The above relation gives a way to convert radians into degrees or degrees into radians.