Definition, Formula, Solved Example Problems, Exercise | Mathematics - Trigonometric Identities | 11th Mathematics : UNIT 3 : Trigonometry
Chapter: 11th Mathematics : UNIT 3 : Trigonometry
Trigonometric Identities
Trigonometric Identities
1. Sum and difference identities or compound angles formulas
Now, compound angles are algebraic sum of two or more angles. Trigonometric functions do not satisfy the functional relations like f(x + y) = f(x) + f(y) and f(kx) = kf(x), k is a real number. For example, cos(α + β) = cos α + cos β, sin(2α) ¹ 2 sin α, tan 3α ¹ 3 tan α, . . .. Thus, we need to derive formulas for sin(α + β), cos(α + β), . . . and use them in calculations of application problems.
Music is made up of vibrations that create pressure on ear-drums. Musical tones can be modeled with sinusoidal graphs (graphs looks like that of y = sin x or y = cos x). When more than one tone is played, the resulting pressure is equal to the sum of the individual pressures. In this context sum and difference trigonometric identities are used as an important application. Also, sum and difference trigonometric identities are helpful in the analysis of waves.
First we shall prove the identity for the cosine of the sum of two angles and extend it to prove all other sum or difference identities.
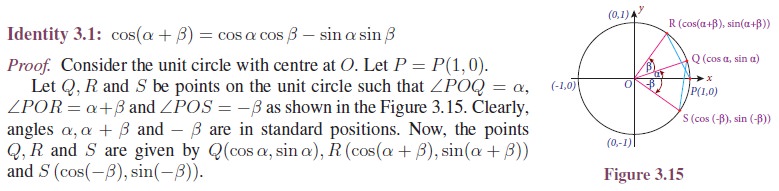



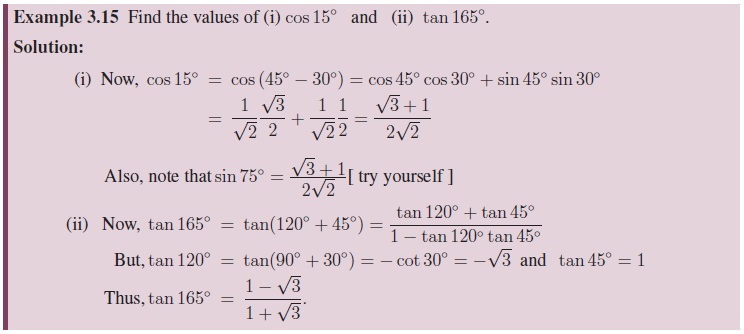

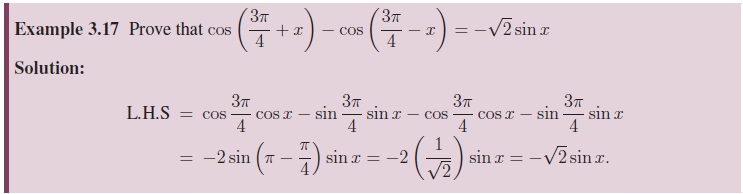


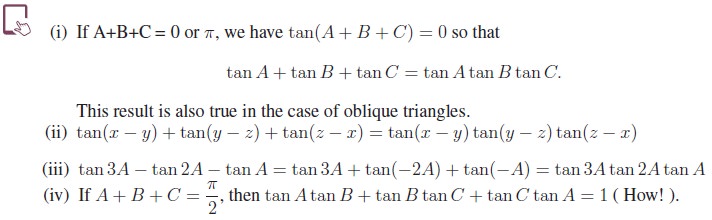
2. Multiple angle identities and submultiple angle identities
In 1831, Michael Faraday discovered that when a wire is passed near a magnet, a small electric current is produced in the wire. This property is used to generate electric current for houses, institutions and business establishments throughout the world. By rotating thousands of wires near large electromagnets, massive amount of electricity can be produced.
Voltage is a quantity that can be modeled by sinusoidal graphs and functions. To model electricity and other phenomena, trigonometric functions and identities involving multiple angles or sub multiple angles are used.
If A is an angle, then 2A, 3A, . . . are called multiple angles of A and the angle A/2 , A/3 , . . .are called sub-multiple angles of A. Now we shall discuss the trigonometric ratio of multiple angles and sub-multiple angles and derive some identities.
Double Angle Identities
Let us take up the sum and difference identities and examine some of the consequences that come from them. Double angle identities are a special case of the sum identities. That is, when the two angles are equal, the sum identities are reduced to double angle identities. They are useful in solving trigonometric equations and also in the verification of trigonometric identities. Further double angle identities can be used to derive the reduction identities (power reducing identities). Also double angle identities are used to find maximum or minimum values of trigonometric expressions.



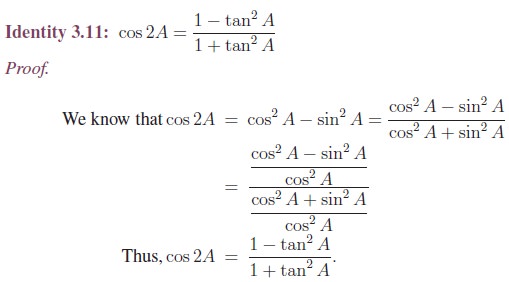
Power reducing identities or Reduction identities
Power reducing identities for sine, cosine and tangent can be derived using the double-angle identities.
For example,

Triple-Angle Identities
Using double angle identities, we can derive triple angle identities.
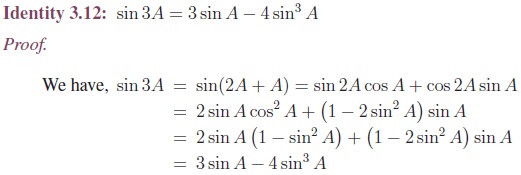


Half-Angle Identities



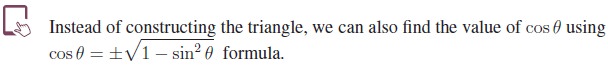
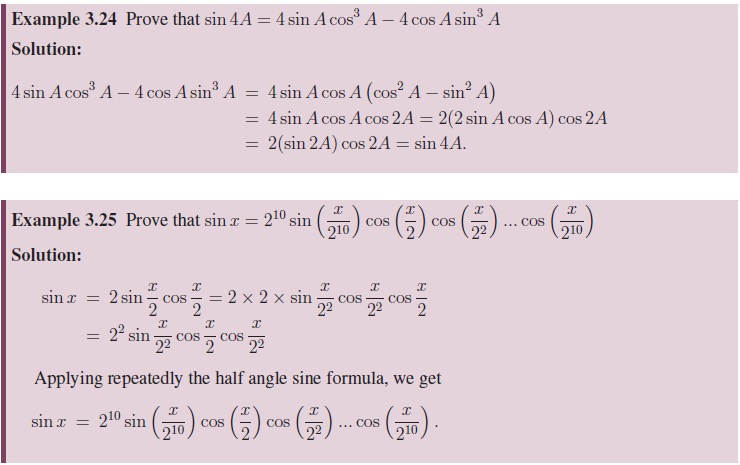



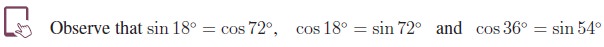
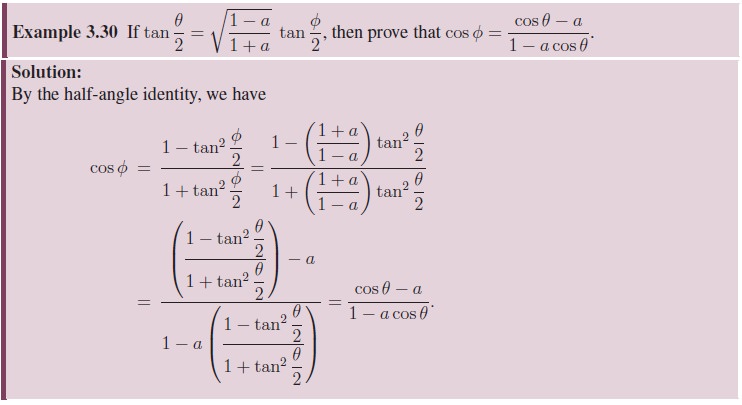



3. Product to Sum and Sum to Product Identities
Some applications of trigonometric functions demand that a product of trigonometric functions be written as sum or difference of trigonometric functions. The sum and difference identities for the cosine and sine functions look amazingly like each other except for the sign in the middle. So, we tend to combine them to get nice identities. Thus, we use them to derive several identities that make it possible to rewrite a product as a sum or a sum as a product.
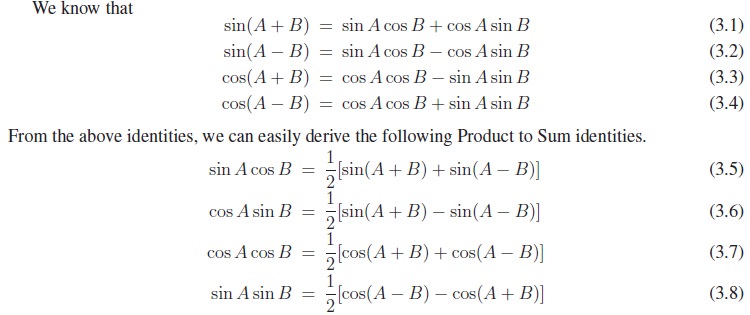
The above identities are very important whenever need arises to transform the product of sine and cosine into sum. This idea is very much useful in evaluation of some integrals.
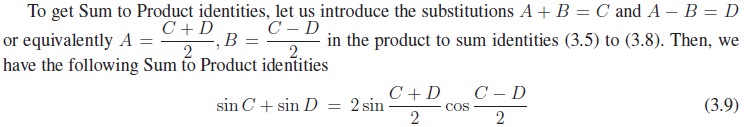

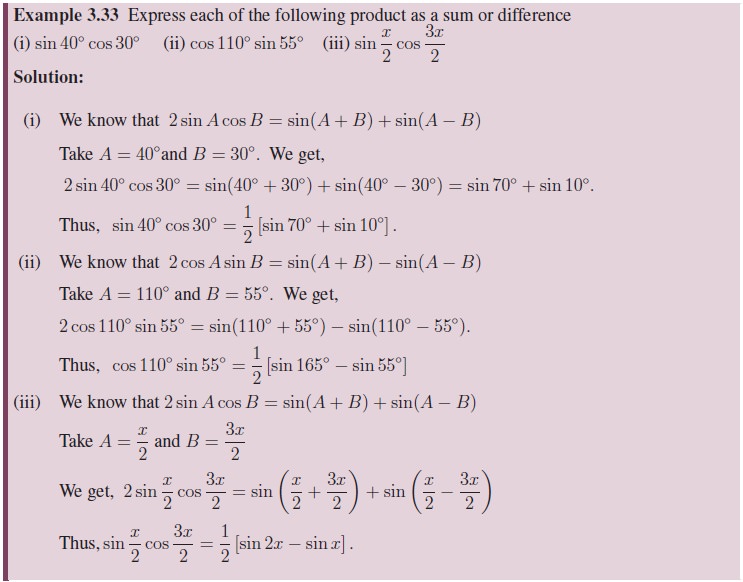

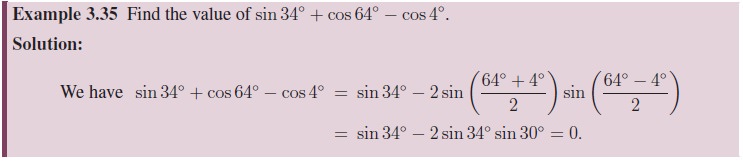

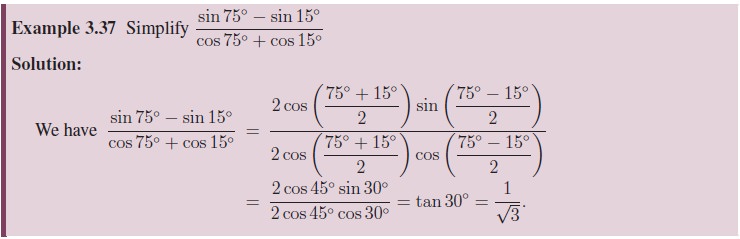

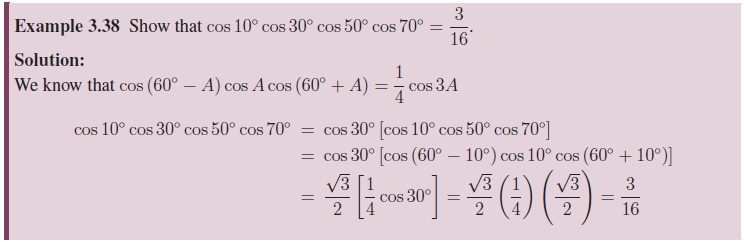

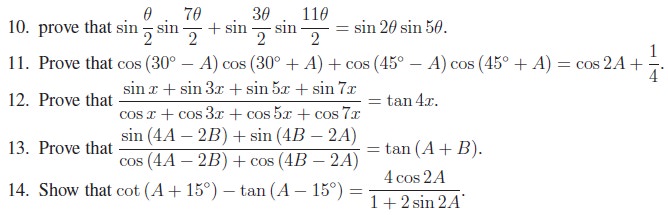
4. Conditional Trigonometric Identities
We know that trigonometric identities are true for all admissible values of the angle involved. There are some trigonometric identities which satisfy the given additional conditions. Such identities are called conditional trigonometric identities.
In this section, we shall make use of the relations obtained in the earlier sections to establish some conditional identities based on some relationship.


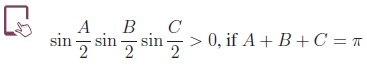
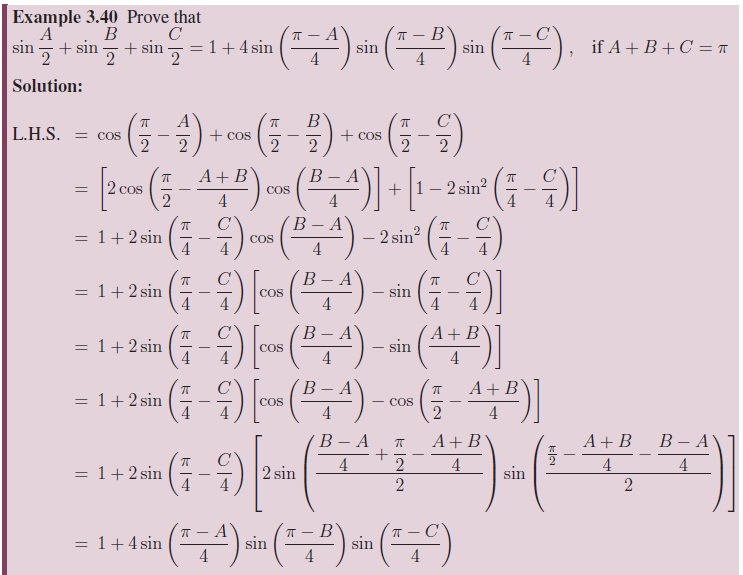

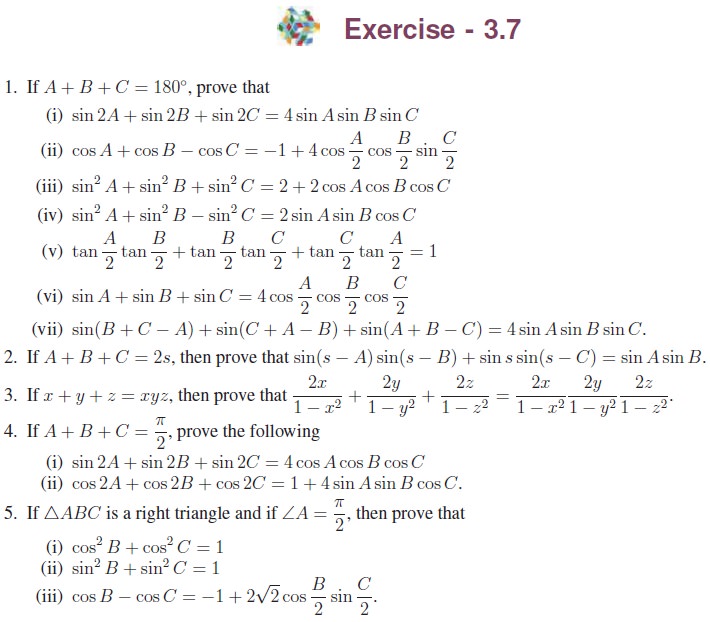
Related Topics