Solved Example Problems, Exercise | Trigonometry | Mathematics - A recall of basic results | 11th Mathematics : UNIT 3 : Trigonometry
Chapter: 11th Mathematics : UNIT 3 : Trigonometry
A recall of basic results
A recall of basic results
In earlier classes, we have
learnt trigonometric ratios using a right triangle and proved trigonometric
identities for an acute angle. One wonders, how the distance between planets,
heights of Mountains, distance between far off objects like Earth and Sun,
heights of tall buildings, the speed of supersonic jets are measured or
calculated. Interestingly, such distances or heights are calculated applying
the trigonometric ratios which were derived for acute angles. Our aim is to
develop trigonometric functions defined for any real number and use them in all
branches of mathematics, in particular, in calculus. First, let us recall the
definition of angle and degree measure of an angle.
1. Angles
The angle AOB is a measure formed by two rays OA and OB sharing the common point O as shown in the Figure 3.1. The common point O is called the vertex of the angle. If we rotate the ray OA about its vertex O and takes the position OB, then OA and OB respectively are called the initial side and the
terminal side of the angle produced. An anticlockwise rotation generates a
positive angle (angle with positive sign), while a clockwise rotation generates
a negative angle (angle with negative sign).

One full anticlockwise (or
clockwise) rotation of OA back to itself is called one complete rotation or revolution.
2. Different Systems of measurement of angle
There are three different systems
for measuring angles.
(i) Sexagesimal system
The Sexagesimal system is the most prevalent
system of measurement where a right angle is divided into 90 equal parts called
Degrees. Each degree is divided into 60 equal parts called Minutes, and each minute into
60 equal parts called
Seconds.
The symbols 1ŌŚ”, 1 and 1 are used to denote a degree, a
minute and a second respectively.
(ii) Centesimal system
In the Centesimal system , the right angle is
divided into 100 equal parts, called Grades; each grade is subdivided into 100 Minutes, and each minute is
subdivided into 100 Seconds. The symbol 1g is used to denote a
grade.
(iii) Circular system
In the circular system , the radian measure
of an angle is introduced using arc lengths in a circle of radius r. Circular system is used in all branches of Mathematics and in
other applications in Science. The symbol 1c is used to denote 1 radian measure.
3. Degree Measure
The degree is a unit of
measurement of angles and is represented by the symbol ŌŚ”. In degrees, we split up one complete rotation into 360 equal
parts and each part is one degree, denoted by 1ŌŚ”. Thus, 1ŌŚ” is 1/360 of one complete rotation. To measure a fraction of an
angle and also for accuracy of measurement of angles, minutes and seconds are introduced. One minute (1 ) corresponds to 1/60 of a degree
and in turn a second (1 ) corresponds to 1/60 of a minute
(or) 1/3600 of a degree.
We shall classify a pair of
angles in the following way for better understanding and usages.
┬Ę
Two angles that have the exact same measure are called congruent
angles.
┬Ę
Two angles that have their measures adding to 90ŌŚ” are called complementary angles.
┬Ę
Two angles that have their measures adding to 180ŌŚ” are called supplementary
angles.
┬Ę
Two angles between 0ŌŚ” and 360ŌŚ” are conjugate if their sum equals 360ŌŚ”.

4. Angles in Standard Position
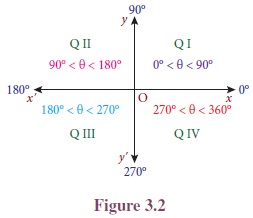
An angle is said to be
in standard position if its vertex is at
the origin and its initial side is along the positive x-axis. An angle is said to be in the first quadrant, if in the
standard position, its terminal side falls in the first quadrant. Similarly, we
can define for the other three quadrants. Angles in standard position having
their terminal sides along the x-axis or y-axis are called quadrantal angles. Thus, 0ŌŚ”, 90ŌŚ”, 180ŌŚ”, 270ŌŚ” and 360ŌŚ” are quadrantal
angles.
5. Coterminal angles
One complete rotation
of a ray in the anticlockwise direc-tion results in an angle measuring of 360ŌŚ”. By continuing the anticlockwise rotation, angles larger than 360ŌŚ” can be produced. If we rotate in clockwise direction, negative
angles are produced. Angles 57ŌŚ”, 417ŌŚ” and ŌłÆ303ŌŚ” have the same initial side and terminal side but with different
amount of rotations, such angles are called coterminal angles. Thus, angles in
standard position that have the same terminal sides are coterminal angles . Hence, if ╬▒ and are coterminal angles, then ╬▓ = ╬▒ + k(360ŌŚ”), k is an integer. The
measurements of coterminal angles differ by an integral multiple of 360ŌŚ”.


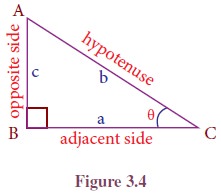
6. Basic Trigonometric ratios using a right triangle
We know that six
ratios can be formed using the three lengths a, b, c of sides of a right
triangle ABC. Interestingly, these ratios lead to the definitions of six
basic trigonometric functions.
First, let us recall
the trigonometric ratios which are defined with reference to a right triangle.

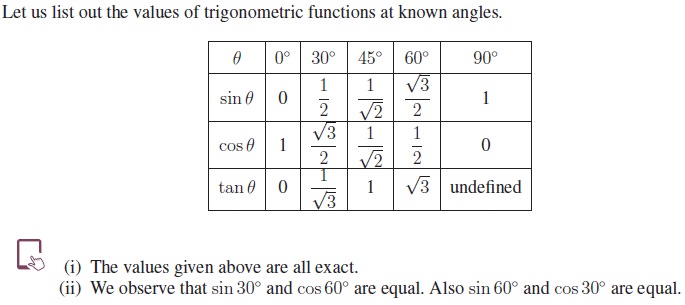
7. Exact values of trigonometric functions of widely used angles

8. Basic Trigonometric Identities



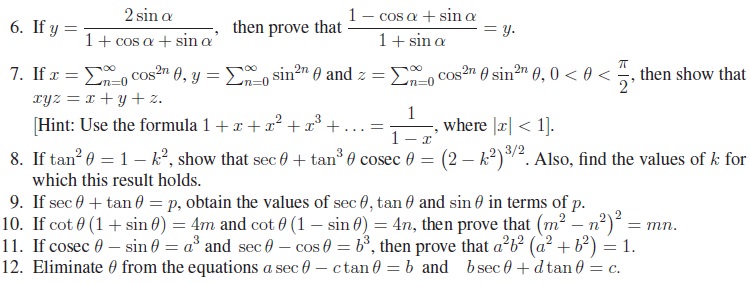
Related Topics