Definition, Formula, Solved Example Problems, Exercise | Mathematics - Inverse Trigonometric Functions | 11th Mathematics : UNIT 3 : Trigonometry
Chapter: 11th Mathematics : UNIT 3 : Trigonometry
Inverse Trigonometric Functions
Inverse Trigonometric Functions
A function f(x) has inverse if
and only if it is one-to-one and onto. Thus, inverse of a function cannot be
defined if it fails to be one-to-one. However, if we restrict the domain
suitably, we can make the function to be one-to-one in the restricted domain.
For example, y = x2 is not one-to-one for all real numbers. But y =
x2 is one-to-one and onto either for x Ōēź 0 or x Ōēż 0. Hence y = x2,
x Ōēź 0 has the inverse f ŌłÆ1(x) = ŌłÜx, x Ōēź 0. Now, owing to their
periodicity, none of six trigonometric functions is one-to-one over their
natural domains. We shall restrict their domains so that trigonometric
functions are one-to-one enabling the existence of their inverse functions.
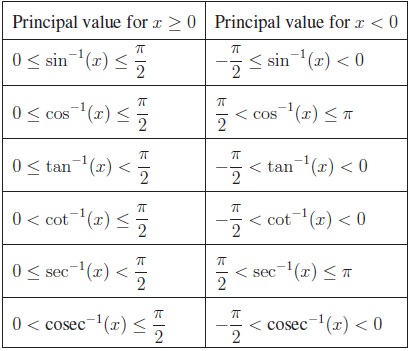
This restriction can be done in many ways once again due to their periodicity.
The conventional choices for the restricted domains are arbitrary but they have
some important characteristics. Each restricted domain includes the number 0
and some positive angles and the image of restricted domain contains the entire
range.




Related Topics