Chemistry - Theories of coordination compound | 12th Chemistry : UNIT 5 : Coordination Chemistry
Chapter: 12th Chemistry : UNIT 5 : Coordination Chemistry
Theories of coordination compound
Theories
of coordination compound
Alfred Werner considered
the bonding in coordination compounds as the bonding between a lewis acid and a
lewis base. His approach is useful in explaining some of the observed
properties of coordination compounds. However, properties such as colour,
magnetic property etc.. of complexes could not be explained on the basis of his
approach. Following werner theory, Linus pauling proposed the Valance Bond
Theory (VBT) which assumes that the bond formed between the central metal atom
and the ligand is purely covalent. Bethe and Van vleck treated the interaction
between the metal ion and the ligands as electrostatic and extended the Crystal
Field Theory (CFT) to explain the properties of coordination compounds.
Further, Ligand field theory and Molecular orbital have been developed to
explain the nature of bonding in the coordination compounds. In this porton we
learn the elementry treatment of VBT and CFT to simple coordination compounds.
1. Valence Bond Theory
According to this
theory, the bond formed between the central metal atom and the ligand is due to
the overlap of filled ligand orbitals containing a lone pair of electron with
the vacant hybrid orbitals of the central metal atom.
Main assumptions of VBT:
1.
The ligand → metal bond in a coordination complex is covalent in
nature. It is formed by sharing of electrons (provided by the ligands) between
the central metal atom and the ligand.
2.
Each ligand should have at least one filled orbital containing a
lone pair of electrons.
3.
In order to accommodate the electron pairs donated by the ligands,
the central metal ion present in a complex provides required number
(coordination number) of vacant orbitals.
4.
These vacant orbitals of central metal atom undergo hybridisation,
the process of mixing of atomic orbitals of comparable energy to form equal
number of new orbitals called hybridised orbitals with same energy.
5.
The vacant hybridised orbitals of the central metal ion, linearly
overlap with filled orbitals of the ligands to form coordinate covalent sigma
bonds between the metal and the ligand.
6.
The hybridised orbitals are directional and their orientation in
space gives a definite geometry to the complex ion.
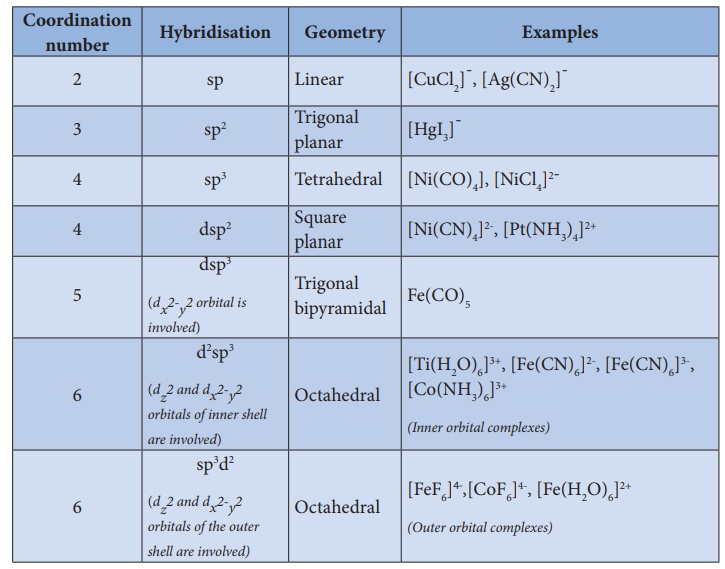
7.
In the octahedral complexes, if the (n-1) d orbitals are involved
in hybridisation, then they are called inner orbital complexes or low spin
complexes or spin paired complexes. If the nd orbitals are involved in
hybridisation, then such complexes are called outer orbital or high spin or
spin free complexes. Here n represents the principle quantum number of the outermost
shell.
8.
The complexes containing a central metal atom with unpaired
electron(s) are paramagnetic. If all the electrons are paired, then the
complexes will be diamagnetic.
9.
Ligands such as CO, CN-, en, and NH3 present
in the complexes cause pairing of electrons present in the central metal atom.
Such ligands are called strong field ligands.
10. Greater the overlapping
between the ligand orbitals and the hybridised metal orbital, greater is the
bond strength.
Let us illustrate the
VBT by considering the following examples.
Illustration 1
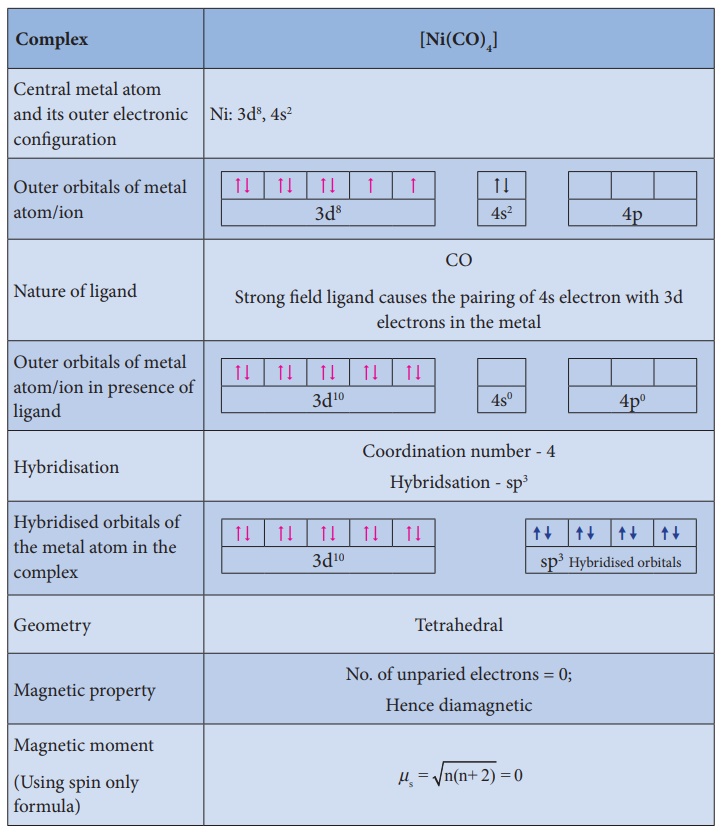
Illustration 2

Illustration 3
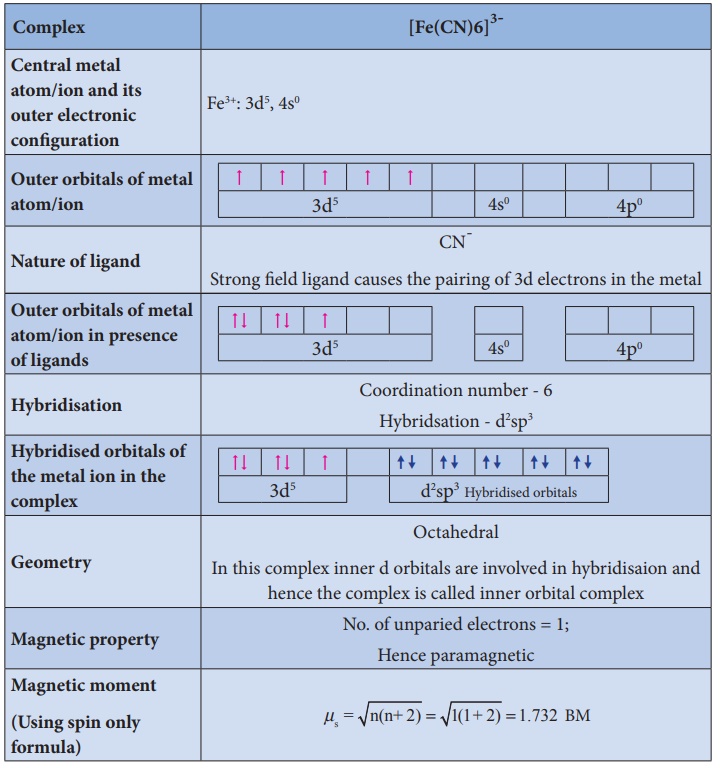
Illustration 4
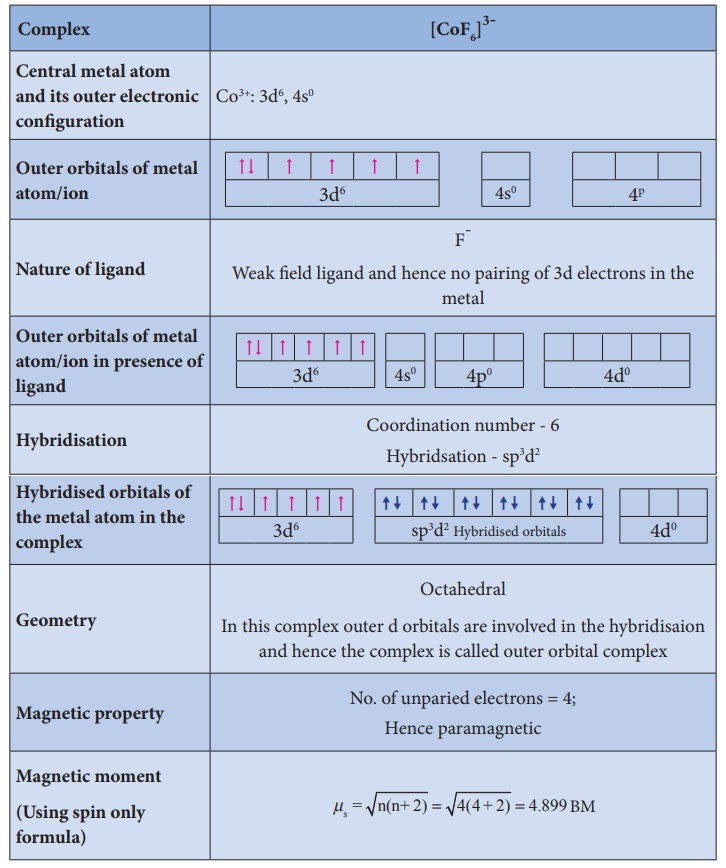
Limitations of VBT
Eventhough VBT explains
many of the observed properties of complexes, it still has following
limitations
1.
It does not explain the colour of the complex
2.
It considers only the spin only magnetic moments and does not
consider the other components of magnetic moments.
3.
It does not provide a quantitative explanation as to why certain
complexes are inner orbital complexes and the others are outer orbital
complexes for the same metal. For example, [Fe(CN)6]4- is
diamagnetic (low spin) whereas [FeF6]4- is paramagnetic
(high spin).
2. Crystal Field Theory
Valance bond theory
helps us to visualise the bonding in complexes. However, it has limitations as
mentioned above.Hence Crystal Field Theory to expalin some of the properties
like colour, magnetic behavior etc.,This theory was originally used to explain
the nature of bonding in ionic crystals. Later on, it is used to explain the
properties of transition metals and their complexes. The salient features of
this theory are as follows.
1.
Crystal Field Theory (CFT) assumes that the bond between the
ligand and the central metal atom is purely ionic. i.e. the bond is formed due
to the electrostatic attraction between the electron rich ligand and the
electron deficient metal.
2.
In the coordination compounds, the central metal atom/ion and the
ligands are considered as point charges (in case of charged metal ions or
ligands) or electric dipoles (in case of neutral metal atoms or ligands).
3.
According to crystal field theory, the complex formation is
considered as the following series of hypothetical steps.
Step 1: In an isolated gaseous
state, all the five d orbitals of the central metal ion are degenerate. Initially, the ligands
form a spherical field of negative charge around the metal. In this filed, the
energies of all the five d orbitals will increase due to the repulsion between
the electrons of the metal and the ligand
Step 2: The ligands are approaching the
metal atom in actual bond directions. To illustrate this let us consider an
octahedral field, in which the central metal ion is located at the origin and
the six ligands are coming from the +x, -x, +y, -y, +z and -z directions as
shown below.
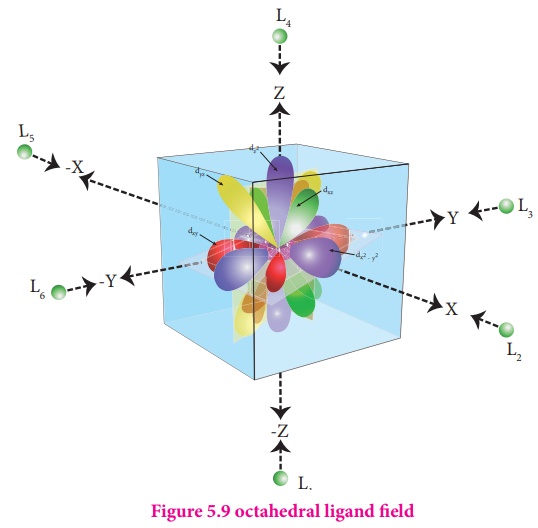
As shown in the figure,
the orbitals lying along the axes dx2-y2 and dz2 orbitals will experience
strong repulsion and raise in energy to a greater extent than the orbitals with
lobes directed between the axes (d xy, dyz and dzx).
Thus the degenerate d orbitals now split into two sets and the process is
called crystal field splitting.
Step 3: Up to this point
the complex formation would not be favoured. However, when the ligands approach
further, there will be an attraction between the negatively charged electron
and the positively charged metal ion, that results in a net decrease in energy.
This decrease in energy is the driving force for the complex formation.
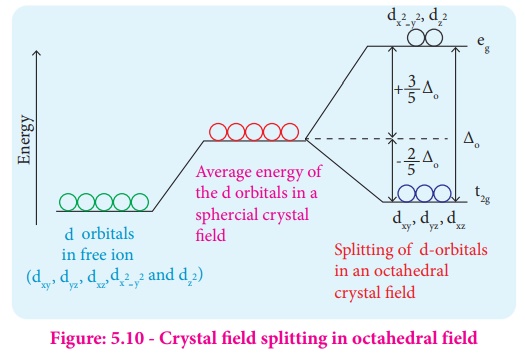
Crystal field splitting in octahedral complexes:
During crystal field
splitting in octahedral field, in order to maintain the average energy of the
orbitals (barycentre) constant, the energy of the orbitals dx2-y2
and dz2 (represented as eg orbitals) will increase by
3/5Δo while that of the other three orbitals dxy, dyz
and dzx (represented as t2g orbitals) decrease by 2/5Δo.
Here, Δo represents the crystal field splitting energy in the
octahedral field.

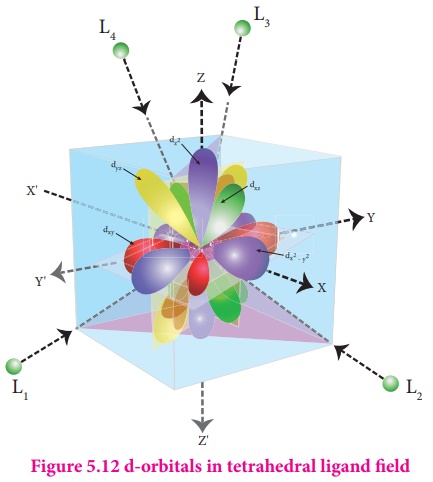
Crystal field splitting in tetrahedral complexes:
The approach of ligands
in tetrahedral field can be visualised as follows. Consider a cube in which the
central metal atom is placed at its centre (i.e. origin of the coordinate axis
as shown in the figure). The four ligands approach the central metal atom along
the direction of the leading diagonals drawn from alternate corners of the
cube.
In this field, none of
the d orbitals point dirctly towards the ligands,however the t2
orbitals (dxy, dyz and dzx) are pointing close
to the direction in which ligands are approaching than the e orbitals (dx2-y2
and d z2).
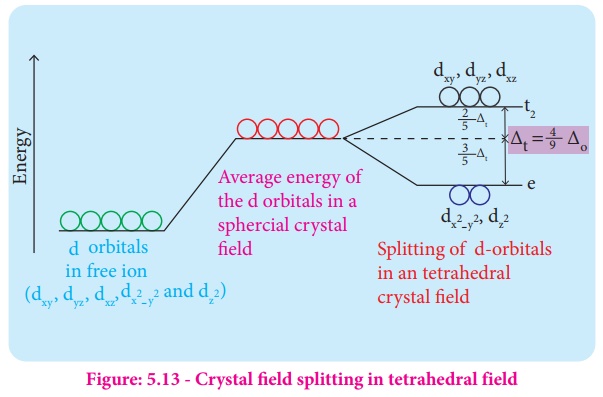
As a result, the energy
of t2 orbitals increases by 2/5Δt and that of e orbitals
decreases by 3/5Δt as shown below. when compared to the octahedral
field, this splitting is inverted and the spliting energy is less. The relation
between the crystal field splitting energy in octahedral and tetrahedral ligand
field is given by the expression; Energy ∆t = 4/9 ∆0
Crystal filed splitting Energy and nature of ligands:
The magnitude of crystal
field splitting energy not only depends on the ligand field as discussed above
but also depends on the nature of the ligand, the nature of the central metal
atom/ion and the charge on it. Let us understand the effect of the nature of
ligand on crystal field splitting by calculating the crystal field splitting
energy of the octahedral complexes of titanium(III) with different ligands such
as fluoride, bromide and water using their absorption spectral data. The
absorption wavelengths of complexes [TiBr 6]3-, [TiF6]3-
and [Ti(H2O)6]3+ are 12500, 19000 and 20000 cm-1
respectively. The energy associated with the absorbed wavelength of light (λ),
corresponds to the crystal field splitting energy (Δ) and is given by the
following expression,
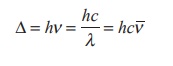
where h is the Plank' s
constant; c is velocity of light, υ is the wave number of absorption
maximum which is equal to 1/λ
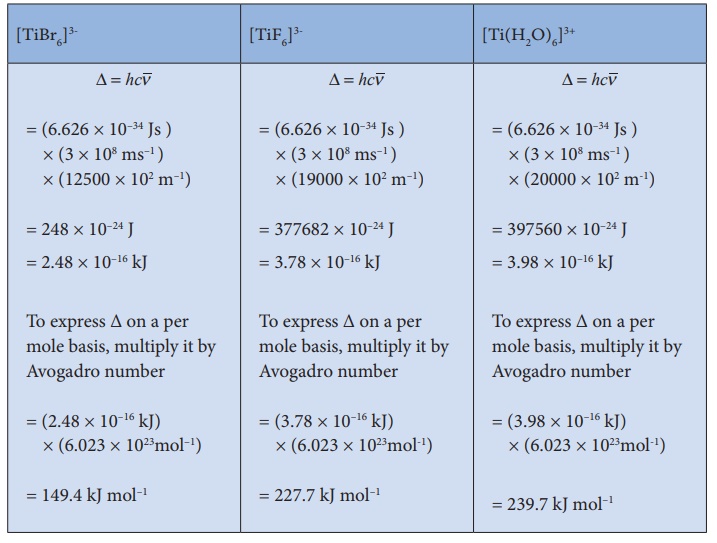
From the above calculations,
it is clear that the crystal filed splitting energy of the Ti3+ in
complexes,the three ligands is in the order; Br- < F-
< H2O. Similarly, it has been found form the spectral data that
the crystal field splitting power of various ligands for a given metal ion, are
in the following order
I-<Br-<SCN-<Cl-<S2-<F-<OH-≈urea<
ox2-< H2O< NCS-<EDTA4-<NH3<en<NO2-<CN-
< CO
The above series is known as spectrochemcial series. The ligands present on the right side of the series such as carbonyl causes relatively larger crystal field splitting and are called strong ligands or strong field ligands, while the ligands on the left side are called weak field ligands and causes relatively smaller crystal field splitting.
Distribution of d electrons in octahedral complexes:
The filling of electrons
in the d orbitals in the presence of ligand field also follows Hund's rule. In
the octahedral complexes with d2 and d3 configurations,
the electrons occupy different degenerate t2g orbitals and remains
unpaired. In case of d4 configuration, there are two possibilities.
The fourth electron may either go to the higher energy eg orbitals
or it may pair with one of the t2g electrons. In this scenario, the
preferred configuration will be the one with lowest energy.
If the octahedral
crystal field splitting energy (Δo) is greater than the pairing
energy (P), it is necessary to cause paring of electrons in an orbital, then
the fourth electron will pair up with an the electron in the t2g
orbital. Conversely, if the Δo is lesser than P, then the fourth
electron will occupy one of the degenerate higher energy eg
orbitals.
For example, let us
consider two different iron(III) complexes [Fe(H2O)6]3+ (weak field
complex; Δo is 14000 cm‑1) and [Fe(CN)6]3-
(Strong field complex; Δo is 35000 cm-1). The pairing energy of
Fe3+ is 30000 cm-1. In both these complexes the Fe3+
has d5 configuration. In aqua complex, the Δo < P
hence, the fourth & fifth electrons enter eg orbitals and the configuration
is t2g3, eg2. In the cyanido
complex Δo > P and hence the fourth & fifth electrons pair up
with the electrons in the t2g orbitals and the electronic
configuration is t2g5, eg0.
The actual distribution
of electrons can be ascertained by calculating the crystal field stabilisation
energy (CFSE). The crystal field stabilisation energy is defined as the energy
difference of electronic configurations in the ligand filed (ELF)
and the isotropic field/barycentre (Eiso).
CFSE (ΔEo) =
{ELF } - {Eiso } = {[nt2g(-0.4)+neg(0.6)]
Δo + npP} - {n'p P}
Here, nt2g is
the number of electrons in t2g orbitals; neg is number of
electrons in eg orbitals; np is number of electron pairs
in the ligand field; & n'p is the number of electron pairs in
the isotropic field (barycentre).
Calculating the CFSE for
the Iron complexes
Complex: [Fe(H2O)6]3+

Complex: [Fe(CN)6]3-

Colour of the complex and crystal field splitting energy:
Most of the transition
metal complexes are coloured. A substance exhibits colour when it absorbs the
light of a particular wavelength in the visible region and transmit the rest of
the visible light. When this transmitted light enters our eye, our brain
recognises its colour. The colour of the transmitted light is given by the
complementary colour of the absorbed light. For example, the hydrated
copper(II) ion is blue in colour as it absorbs orange light, and transmit its
complementary colour, blue. A list of absorbed wavelength and their
complementary colour is given in the following table.
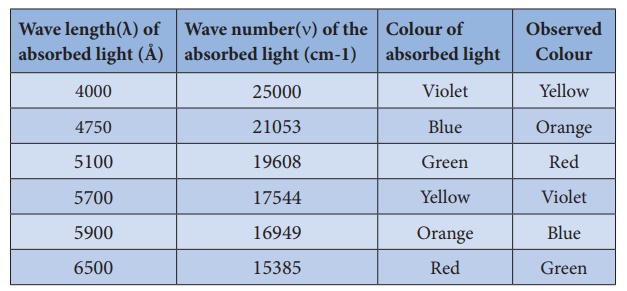

The observed colour of a
coordination compound can be explained using crystal field theory. We learnt
that the ligand field causes the splitting of d orbitals of the central metal
atom into two sets (t2g and eg). When the white light
falls on the complex ion, the central metal ion absorbs visible light
corresponding to the crystal filed splitting energy and transmits rest of the
light which is responsible for the colour of the complex.
This absorption causes
excitation of d-electrons of central metal ion from the lower energy t2g
level to the higher energy eg level which is known as d-d
transition.
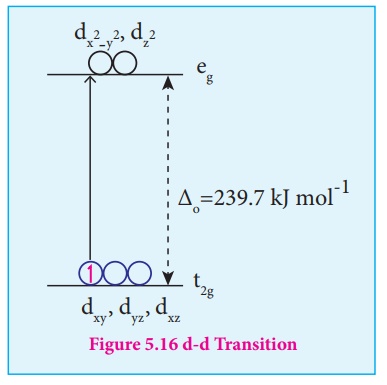
Let us understand the
d-d transitions by considering [Ti(H2O)6]3+ as
an example. In this complex the central metal ion is Ti3+, which has
d1 configuration. This single electron occupies one of the t2g
orbitals in the octahedral aqua ligand field. When white light falls on this
complex the d electron absorbs light and promotes itself to eg
level. The spectral data show the absorption maximum is at 20000 cm-1
corresponding to the crystal field splitting energy (Δo) 239.7 kJ
mol-1. The transmitted colour associated with this absorption is
purple and hence ,the complex appears purple in colour.
The octahedral titanium (III)
complexes with other ligands such as bromide and fluoride have different
colours. This is due to the difference in the magnitude of crystal field
splitting by these ligands. However, the complexes of central metal atom such
as of Sc3+, Ti4+, Cu+, Zn2+, etc...
are colourless. This is because the d-d transition is not possible in complexes
with central metal having d0 or d10 configuration.
Metallic carbonyls
Metal carbonyls are the
transition metal complexes of carbon monoxide, containing Metal-Carbon bond. In
these complexes CO molecule acts as a neutral ligand. The first homoleptic
carbonyl [Ni(CO)4] nickel tetra carbonyl was reported by Mond in
1890.These metallic carbonyls are widely studied because of their industrial
importance, catalytic properties and their ability to release carbon monoxide.
Classification:
Generally metal
carbonyls are classified in two different ways as described below.
(i) Classification based on the number of metal atoms present.
Depending upon the
number of metal atoms present in a given metallic carbonyl, they are classified
as follows.
a. Mononuclear carbonyls
These compounds contain
only one metal atom, and have comparatively simple structures. For
example, [Ni (CO)4] - nickel tetracarbonyl is tetrahedral, [ Fe (CO)5
] - Iron pentacarbonyl is
trigonalbipyramidal, and [ Cr (CO)6] - Chromium hexacarbonyl is
octahedral.
b. Poly nuclear carbonyls
Metalliccarbonylscontainingtwoormoremetalatomsarecalledpolynuclearcarbonyls.Poly
nuclear metal carbonyls may be Homonuclear ([Co2 (CO)8 ],
[ Mn2 (CO)10 ], [ Fe3 (CO)12]) or hetero nuclear ([MnCo (CO)9],
MnRe(CO)10]) etc.
(ii) Classification based on the structure:
The structures of the
binuclear metal carbonyls involve either metal–metal bonds or bridging CO
groups, or both. The carbonyl ligands that are attached to only one metal atom
are referred to as terminal carbonyl groups, whereas those attached to
two metal atoms simultaneously are called bridging carbonyls. Depending
upon the structures, metal carbonyls are classified as follows.
a. Non-bridged metal carbonyls:
These metal carbonyls do
not contain any bridging carbonyl ligands. They may be of two types.
(i) Non- bridged metal
carbonyls which contain only terminal carbonyls. Examples:
[Ni (CO)4 ,[ Fe (CO)5 and [ Cr (CO)6]

(ii) Non- bridged metal
carbonyls which contain terminal carbonyls as well as Metal-Metal bonds. For examples,The structure of Mn2(CO)10
actually involve only a metal–metal bond,
so the formula is more correctly represented as (CO)5Mn−Mn(CO)5.

Other examples of this
type are,Tc2(CO)10, and Re2(CO)10.
b. Bridged carbonyls:
These metal carbonyls
contain one or more bridging carbonyl ligands along with terminal carbonyl
ligands and one or more Metal-Metal bonds. For example,
(i) The structure of Fe2(CO)9,
di-iron nona carbonyl molecule consists of three bridging CO ligands, six
terminal CO groups
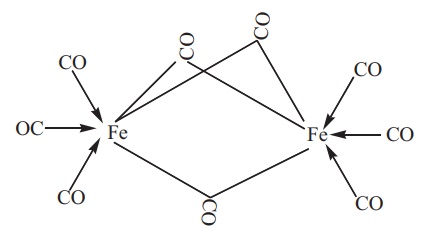
(ii) For
dicobaltoctacarbonyl Co2(CO)8two isomers are possible.
The one has a metal–metal bond between the cobalt atoms, and the other has two
bridging CO ligands.
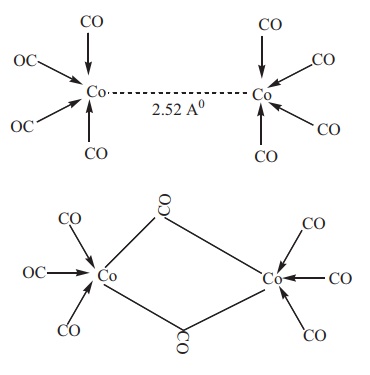
Bonding in metal carbonyls
In metal carbonyls, the
bond between metal atom and the carbonyl ligand consists of two components. The
first component is an electron pair donation from the carbon atom of carbonyl
ligand into a vacant d-orbital of central metal atom. This electron pair
donation forms M ← σbond ←CO
sigma bond. This sigma bond formation increases the electron density in metal d
orbitals and makes the metal electron rich. In order to compensate for this
increased electron density, a filled metal d-orbital interacts with the empty
π* orbital on the carbonyl ligand and transfers the added electron density back
to the ligand. This second component is called π-back bonding . Thus in metal
carbonyls, electron density moves from ligand to metal through sigma bonding
and from metal to ligand through pi bonding, this synergic effect accounts for
strong M ← CO bond in metal carbonyls.
This phenomenon is shown diagrammatically as follows.
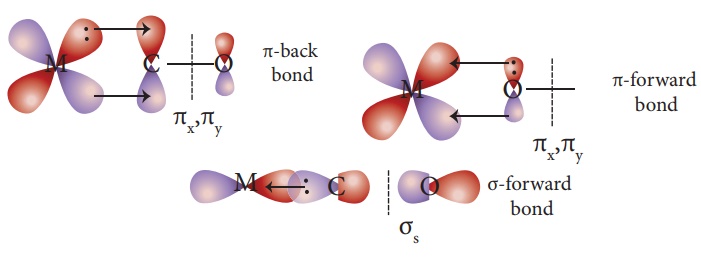
Related Topics