The Switched Capacitor Filter

The Switched Capacitor Filter

Basic Representation:

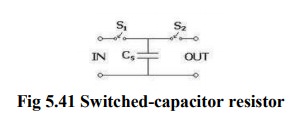
The simplest switched capacitor (SC) circuit is the switched capacitor resistor, made of one capacitor C and two switches S1 and S2 which connect the capacitor with a given frequency alternately to the input and output of the SC. Each switching cycle transfers a charge q from the input to the output at the switching frequency f. Recall that the charge q on a capacitor C with a voltage V between the plates is given by:

q=CV

where V is the voltage across the capacitor. Therefore, when S1 is closed while S2 is open, the charge transferred from the source to CS is:

q_IN=C_SV_IN

And when S₂ is closed while S₁ is open, the charge transferred from CS to the load is:

q_OUT = C_SV_OUT

Thus, the charge transferred in each cycle is:

Q=q_OUT-q_IN=C_s(V_OUT-V_IN)

Since a charge q is transferred at a rate f, the rate of transfer of charge per unit time is:

I=qf

Note that we use I, the symbol for electric current, for this quantity. This is to demonstrate that a continuous transfer of charge from one node to another is equivalent to a current. Substituting for q in the above, we have:

I=C_s(V_OUT-V_IN)f

Let us define V, the voltage across the SC from input to output, thus:

V=V_OUT-V_IN

We now have a relationship between I and V, which we can rearrange to give an equivalent resistance R:

R=V/I=1/C_sf

Thus, the SC behaves like a resistor whose value depends on CS and f.

The SC resistor is used as a replacement for simple resistors in integrated circuits because it is easier to fabricate reliably with a wide range of values. It also has the benefit that its value can be adjusted by changing the switching frequency. See also: operational amplifier applications.

This same circuit can be used in discrete time systems (such as analog to digital converters) as a track and hold circuit. During the appropriate clock phase, the capacitor samples the analog voltage through switch one and in the second phase presents this held sampled value to an electronic circuit for processing.

Switched Capacitor Circuits:

The switched capacitor filter allows for very sophisticated, accurate, and tuneable analog circuits to be manufactured without using resistors.

Advantages: resistors are hard to build on integrated circuits (they take up a lot of room), and the circuits can be made to depend on ratios of capacitor values (which can be set accurately), and not absolute values (which vary between manufacturing runs).

The Switched Capacitor Resistor:

Consider the circuit shown with a capacitor connected to two switches and two different voltages.

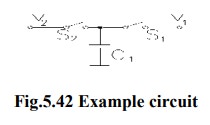
If S2 closes with S1 open, then S1 closes with switch S2 open, a charge (q is transferred from V₂ to  V₁ with

∆q=C1(v₂-v₁)

If this switching process is repeated N times in a time (t, the amount of charge transferred per unit time is given by

∆q/∆t=C₁(v₂-v₁)  N/∆t

the number of cycles per unit time is the switching frequency (or clock frequency, f_CLK)

i= C₁(v₂-v₁) f_CLK

Rearranging we get

(v₂-v₁) / I = [ 1/ C₁ f_CLK ] -R

Which states that the switched capacitor is equivalent to a resistor? The value of this resistor decreases with increasing switching frequency or increasing capacitance, as either will increase the amount of charge transferred from V₂ to  V₁ in a given time.

The Switched Capacitor Integrator:

Now consider the integrator circuit. You have shown (in a previous lab) that the input-output relationship for this circuit is given by (neglecting initial conditions):

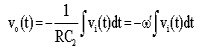
We can also write this with the "s" notation (assuming a sinusoidal input, Ae^st, s=jω)

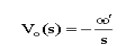
If you replaced the input resistor with a switched capacitor resistor, you would get

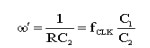
Thus, you can change the equivalent ω' of the circuit by changing the clock frequency. The value of ω' can be set very precisely because it depends only on the ratio of C1 and C2, and not their absolute value.

Switched Capacitor Filter ICs:

Some of the Switched capacitor filter ICs is MF 5, MF10 and MF100

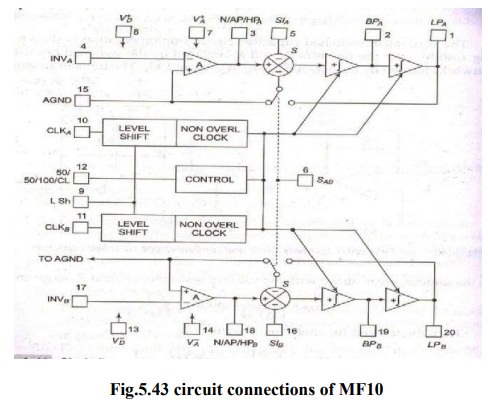
MF10:

The MF10 contains two of the second-order universal filter sections found in the MF5. Therefore with MF10, two second order filters or one fourth-order filter can be built. As the MF5 and MF10 have similar filter sections, the design procedure for them is same.