Basics of Oscillators: Criteria for oscillation

Basics of Oscillators: Criteria for oscillation:

The canonical form of a feedback system is shown in Figure 5 . 1, and Equation 1 describes the performance of any feedback system (an amplifier with passive feedback Components constitute a feedback system).

Oscillation results from an unstable state; i.e., the feedback system can’t find a stable state because its transfer function can’t be satisfied. Equation 1 becomes unstable when (1+Aβ) = 0 because A/0 is an undefined state. Thus, the key to designing an oscillator is to insure that Aβ = –1 (called the Barkhausen criterion), or using complex math the equivalent expression is Aβ = 1 –180°. The 180° phase shift criterion applies to negative feedback systems, and 0° phase shift applies to positive feedback systems.

The output voltage of a feedback system heads for infinite voltage when Aβ = –1. When the output voltage approaches either power rail, the active devices in the amplifiers change gain, causing the value of A to change so the value of Aβ ≠1; thus, the charge to infinite voltage slows down and eventually halts. At this point one of three things can occur.

First, nonlinearity in saturation or cutoff can cause the system to become stable and lock

up.

Second, the initial charge can cause the system to saturate (or cut off) and stay that way for a long time before it becomes linear and heads for the opposite power rail.

Third, the system stays linear and reverses direction, heading for the opposite power rail. Alternative two produces highly distorted oscillations (usually quasi square waves), and the resulting oscillators are called relaxation oscillators. Alternative three produces sine wave oscillators.

Phase Shift in Oscillators:

The 180° phase shift in the equation Aβ = 1        –180° is introduced by active and passive components. The phase shift contributed by  active components is minimized because it varies with temperature, has a wide initial tolerance, and is device dependent.

Amplifiers are selected such that they contribute little or no phase shift at  the oscillation frequency. A single pole RL or RC circuit contributes up to 90° phase shift per pole,  and because 180° is required for oscillation, at least two poles must be used in oscillator design.

An LC circuit has two poles; thus, it contributes up to 180° phase shift per pole pair, but LC and LR oscillators are not considered here because low frequency inductors are expensive, heavy, bulky, and non-ideal. LC oscillators are designed in high frequency applications beyond the frequency range of voltage feedback op amps, where the inductor size, weight, and cost are less significant.

Multiple RC sections are used in low-frequency oscillator design in lieu of inductors. Phase shift determines the oscillation frequency because the circuit oscillates at the frequency that accumulates –180° phase shift. The rate of change of phase with frequency, dS/dt, determines frequencystability.

When buffered RC sections (an op amp buffer provides high input and low output impedance) are cascaded, the phase shift multiplies by the number of sections, n (see Figure 2).

Although two cascaded RC sections provide 180° phase shift, dS/dt at the oscillator frequency is low, thus oscillators made with two cascaded RC sections have poor frequency stability. Three equal cascaded RC filter sections have a higher dS/dt, and the resulting oscillator has improved frequency stability.

Adding a fourth RC section produces an oscillator with an excellent dS/dt, thus this is the most stable oscillator configuration. Four sections are the maximum number used

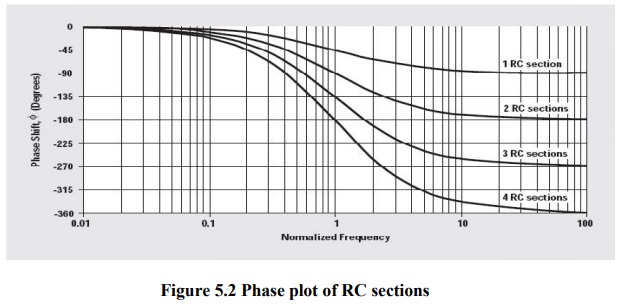
because op amps come in quad packages, and the four-section oscillator yields four sine waves that are 45° phase shifted relative to each other, so this oscillator can be used to obtain sine/cosine or quadrature sine waves.

Applications

Crystal or ceramic resonators make the most stable oscillators because resonators have an extremely high dS/dt resulting from their non-linear properties.

Resonators are used for high- frequency oscillators, but low-frequency oscillators do not use resonators because of size, weight, and cost restrictions.

Op amps are not used with crystal or ceramic resonator oscillators because op amps have low bandwidth. It is more cost-effective to build a high- frequency crystal oscillator and count down the output to obtain a low frequency than it is to use a low-frequency resonator.

Gain in Oscillators:

The oscillator gain must equal one (Aβ = 1–180°) at the oscillation frequency. The circuit becomes stable when the gain exceeds one and oscillations cease. When the gain exceeds one with a phase shift of –180°, the active device non-linearity reduces the gain to one.

The non-linearity happens when the amplifier swings close to either power rail because cutoff or saturation reduces the active device (transistor) gain. The paradox is that worst-case design practice requires nominal gains exceeding one for manufacturability, but excess gain causes more distortion of the output sine wave.

When the gain is too low, oscillations cease under worst-case conditions, and when the gain is too high, the output wave form looks more like a square wave than a sine wave.

Distortion is a direct result of excess gain overdriving the amplifier; thus, gain must be carefully controlled in low distortion oscillators.

Phase-shift oscillators have distortion, but they achieve low-distortion output voltages because cascaded RC sections act as distortion filters. Also, buffered phase-shift oscillators have low distortion because the gain is controlled and distributed among the buffers.