The Digital Comparator

The Digital Comparator

Another common and very useful combinational logic circuit is that of the Digital Comparator circuit. Digital or Binary Comparators are made up from standard AND, NOR and NOT gates that compare the digital signals present at their input terminals and produce an output depending upon the condition of those inputs. For example, along with being able to add and subtract binary numbers we need to be able to compare them and determine whether the value of input A is greater than, smaller than or equal to the value at input B etc. The digital comparator accomplishes this using several logic gates that operate on the principles of Boolean algebra. There are two main types of digital comparator available and these are.

Identity Comparator - is a digital comparator that has only one output terminal for when A = B either "HIGH" A = B = 1 or "LOW" A = B = 0

Magnitude Comparator - is a type of digital comparator that has three output terminals, one each for equality, A = B greater than, A > B and less than A < B

The purpose of a Digital Comparator is to compare a set of variables or unknown numbers, for example A (A1, A2, A3, .... An, etc) against that of a constant or unknown value such as B (B1, B2, B3, .... Bn, etc) and produce an output condition or flag depending upon the result of the comparison. For example, a magnitude comparator of two 1-bits, (A and B) inputs would produce the following three output conditions when compared to each other.

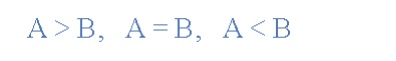
This is useful if we want to compare two variables and want to produce an output when any of the above three conditions are achieved. For example, produce an output from a counter when a certain count number is reached. Consider the simple 1-bit comparator below.

1-bit Comparator

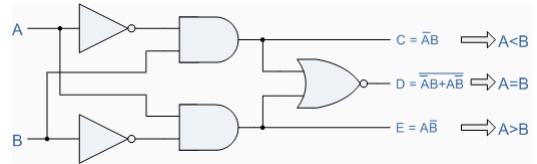
Then the operation of a 1-bit digital comparator is given in the following Truth Table.

Truth Table

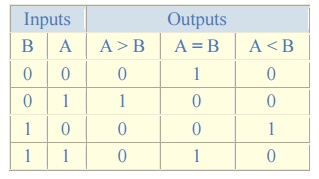
You may notice two distinct features about the comparator from the above truth table. Firstly, the circuit does not distinguish between either two "0" or two "1"'s as an output A = B is produced when they are both equal, either A = B = "0" or A = B  = "1". Secondly, the output condition for A = B resembles that of a You may notice two distinct features about the comparator from the above truth table. Firstly, the circuit does not distinguish between either two "0" or two "1"'s as an output A = B is produced when they are both equal, either A = B = "0" or A = B = "1". Secondly, the output condition for A = B resembles that of a commonly available logic gate, the Exclusive-NOR or Ex-NOR function (equivalence) on each of the n-bits giving: Q = A ⊕ B

Digital comparators actually use Exclusive-NOR gates within their design for comparing their respective pairs of bits. When we are comparing two binary or BCD values or variables against each other, we are comparing the "magnitude" of these values, a logic "0" against a logic "1" which is where the term Magnitude Comparator comes from.

As well as comparing individual bits, we can design larger bit comparators by cascading together n of these and produce a n-bit comparator just as we did for the n-bit adder in the previous tutorial. Multi-bit comparators can be constructed to compare whole binary or BCD words to produce an output if one word is larger, equal to or less than the other. A very good example of this is the 4-bit Magnitude Comparator. Here, two 4-bit words ("nibbles") are compared to each other to produce the relevant output with one word connected to inputs A and the other to be compared against connected to input B as shown below.

4-bit Magnitude Comparator

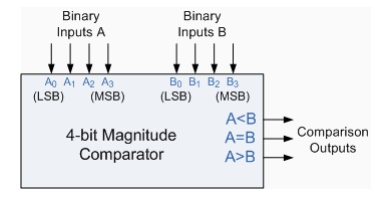
Some commercially available digital comparators such as the TTL 7485 or CMOS 4063 4-bit magnitude comparator have additional input terminals that allow more individual comparators to be "cascaded" together to compare words larger than 4-bits with magnitude comparators of "n"-bits being produced. These cascading inputs are connected directly to the corresponding outputs of the previous comparator as shown to compare 8, 16 or even 32-bit words.