Chapter: Biochemistry: The Importance of Energy Changes and Electron Transfer in Metabolism
Standard States for Free-Energy Changes
Standard States for Free-Energy
Changes
We have already seen, how the lowering of energy, which really
means dispersal on the molecular level, is spontaneous in the thermodynamic
sense. In this, we are going to see how energetic considerations apply to
metabolism. We are going to be comparing so many different processes that it
will be useful to have a benchmark against which to make those comparisons.
What are standard states?
We can deÞne standard
conditions for any process and then use those standard conditions as the
basis for comparing reactions. The choice of standard conditions is arbitrary.
For a process under standard conditions, all substances involved in the
reaction are in their standard states,
in which case they are also said to be at unit
activity. For pure solids and pure liquids, the standard state is the pure
substance itself. For gases, the standard state is usually taken as a pressure
of 1.00 atmosphere of that gas. For solutes, the standard state is usually
taken as 1.00 molar concentration. Strictly speaking, these deÞnitions for
gases and for solutes are approximations, but they are valid for all but the
most exacting work.
What do standard states have to do with free-energy changes?
For any general reaction
a A + b B
-- > C + d D
we can write an equation that relates the free-energy change ( G) for the reaction under any conditions to the free-energy change
under standard conditions ( ∆G°); the superscript ¡ refers to
standard conditions. This equation is
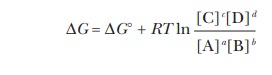
In this equation, the square brackets indicate molar
concentrations, R is the gas constant
(8.31 J mol-1 K-1), and T is the absolute
temperature. The notation ln refers to natural logarithms (to the base e) rather than logarithms to the base
10, for which the notation is log. This equation holds under all circumstances;
the reaction does not have to be at equilibrium. The value of G under a given set of conditions
depends on the value of ∆G° and on
the concentration of reactants and products (given by the second term in the
equation). Most biochemical reactions are described in terms of ∆G°, which is the G under standard conditions (1.00 M concentration for solutes). There is only one ∆G° for a reaction at a given
temperature.
When the reaction is at equilibrium, ∆G = 0, and thus
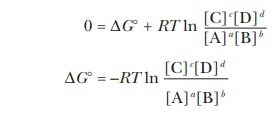
The concentrations are now equilibrium concentrations, and this
equation can be rewritten
∆G° = -RT ln
Keq
where Keq is the
equilibrium constant for the reaction. We now have a relationship between the
equilibrium concentrations of reactants and products and the standard
free-energy change. After we have determined the equilibrium concentrations of
reactants by any convenient method, we can calculate the equilibrium constant, Keq. We can
then calculate the standard free-energy change, ∆G°, from the equilibrium constant.
Summary
Standard states are benchmark conditions chosen to have a basis of
comparison for energy changes in processes under a wide variety of conditions.
Free-energy changes under standard conditions can be related to
free-energy changes under any condition by a well-known equation.
Related Topics