Chapter: Communication Theory : Information Theory
Source Coding
SOURCE CODING:
A code is
defined as an n-tuple of q elements. Where q is any alphabet. Ex. 1001 n=4,
q={1,0} Ex.
2389047298738904
n=16, q={0,1,2,3,4,5,6,7,8,9} Ex. (a,b,c,d,e) n=5, q={a,b,c,d,e,…,y,z} The most
common code is when q={1,0}. This is known as a binary code. The purpose A
message can become distorted through a wide range of unpredictable errors.
• Humans
• Equipment
failure
• Lighting
interference
• Scratches
in a magnetic tape
Ø Error-correcting code:
To add
redundancy to a message so the original message can be recovered if it has been
garbled.
e.g. message = 10 code = 1010101010
Ø Send a message:

Ø Source Coding loss:
It may
consider semantics of the data depends on characteristics of the data e.g. DCT,
DPCM, ADPCM, color model transform A code is distinct if each code word can be
distinguished from every other (mapping is one-to-one) uniquely decodable if
every code word is identifiable when immersed in a sequence of code words e.g.,
with previous table, message 11 could be defined as either ddddd or bbbbbb
Measure of Information Consider symbols si and the probability of occurrence of
each symbol p(si)
Example
Alphabet = {A, B} p(A) = 0.4; p(B) = 0.6 Compute Entropy (H) -0.4*log2 0.4 + -
0.6*log2 0.6 = .97 bits Maximum uncertainty (gives largest H) occurs when all
probabilities are equal Redundancy Difference between avg. codeword length (L)
and avg. information content (H) If H is constant, then can just use L Relative
to the optimal value
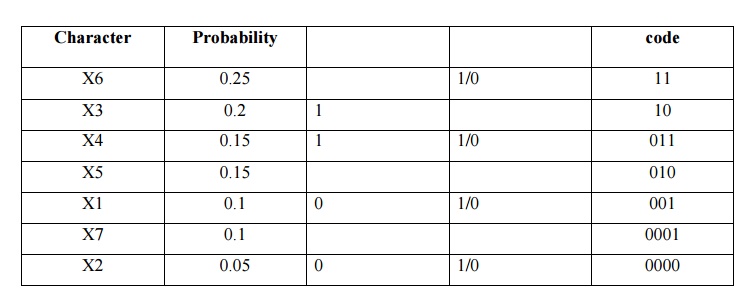
Ø Shannon-Fano Algorithm:
•
Arrange the character set in order of decreasing
probability
•
While a probability class contains more than one
symbol:
ü Divide
the probability class in two so that the probabilities in the two halves are as
nearly as possible equal.
ü Assign a
'1' to the first probability class, and a '0' to the second
TABLE :
5.1
Ø Huffman Encoding:
Statistical
encoding To determine Huffman code, it is useful to construct a binary tree
Leaves are characters to be encoded Nodes carry occurrence probabilities of the
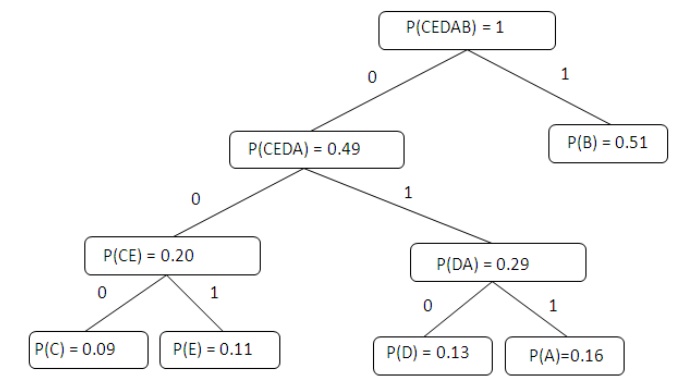
characters belonging to the subtree Example: How does a Huffman code look like
for symbols with statistical symbol occurrence probabilities: P(A) = 8/20, P(B)
= 3/20, P(C ) = 7/20, P(D) = 2/20? Step 1 : Sort all Symbols according to their
probabilities (left to right) from Smallest to largest these are the leaves of
the Huffman tree Step 2: Build a binary tree from left toRight Policy: always
connect two smaller nodes together (e.g., P(CE) and P(DA) had both
Probabilities that were smaller than P(B), Hence those two did connect first
Step 3: label left branches of the tree With 0 and right branches of the tree
With 1 Step 4: Create Huffman Code Symbol A = 011 Symbol B = 1 Symbol C = 000
Symbol D = 010 Symbol E = 001
Related Topics