Shannon-Hartley Theorem

SHANNON–HARTLEY THEOREM:

In information theory, the Shannon–Hartley theorem tells the maximum rate at which information can  be  transmitted  over  a  communications  channel  of  a specified bandwidth in the presence of noise.  It  is  an  application  of  the noisy channel  coding theorem to the  archetypal case  of a continuous-time analog communications channel subject to Gaussian noise. The theorem  establishes Shannon's channel capacity for such a communication link, a bound on the maximum amount of error-free digital data (that is, information) that can be transmitted with a specified bandwidth in the presence of the noise interference, assuming that the signal power is bounded, and that the Gaussian noise process is characterized by a known power or power spectral density. The law is named after Claude Shannon and Ralph Hartley.

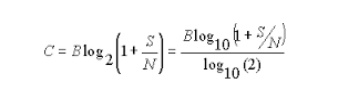
Considering all possible multi-level and multi-phase encoding techniques, the Shannon–Hartley theorem states the channel capacity C, meaning the theoretical tightest upper bound on the information rate (excluding error correcting codes) of clean (or arbitrarily low bit error rate) data that can be sent with a given average signal power S through an analog communication channel subject to additive white Gaussian noise of power N, is:

Where C is the channel capacity in bits per second;

B is the bandwidth of the channel in hertz (passband bandwidth in case of a modulated signal);

S is the average received signal power over the bandwidth (in case of a modulated signal, often denoted C, i.e. modulated carrier), measured in watts (or volts squared);

N is the average noise or interference power over the bandwidth, measured in watts (or volts squared); and

S/N is the signal-to-noise ratio (SNR) or the carrier-to-noise ratio (CNR) of the communication signal to the Gaussian noise interference expressed as a linear power ratio (not as logarithmic decibels).

APPLICATION & ITS USES:

1.     Huffman coding is not always optimal among all compression methods.

2.     Discrete memory less channels.

3.     To find 100% of efficiency using these codings.