Chapter: Communication Theory : Information Theory
Entropy
ENTROPY:
Entropy is the average amount of information contained in each message received.
Here, message stands for an event, sample or character drawn
from a distribution or data stream. Entropy thus characterizes our uncertainty
about our source of information. (Entropy is best understood as a measure of
uncertainty rather than certainty as entropy is larger for more random
sources.) The source is also characterized by the probability distribution of
the samples drawn from it.
ü Formula for
entropy:
Information strictly in terms of the probabilities of events. Therefore, let us suppose that we have a set of probabilities (a probability distribution) P = {p1, p2, . . . , pn}. We define entropy of the distribution P by
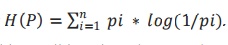
. Shannon defined the entropy of the a discrete random
variable X with possible values {x1, ..., xn} and probability mass function P(X) as: Here E is the expected
value operator, and I is the information content of X. I(X) is itself a random
variable. One may also define the conditional entropy of two events X and Y
taking values xi and yj respectively, as
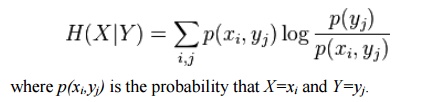
ü Properties:
·
If X and Y are two independent experiments, then
knowing the value of Y doesn't
influence our knowledge of the value of X
(since the two don't influence each other by independence):

·
The entropy of two simultaneous events is no more
than the sum of the entropies of each individual event, and are equal if the
two events are independent. More specifically, ifX and Y are two random
variables on the same probability space, and (X,Y) denotes their Cartesian product, then
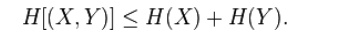
Related Topics