Chapter: Communication Theory : Information Theory

Huffman Coding

The Shannon–Fano algorithm doesn't always generate an optimal code. In 1952, David A. Huffman gave a different algorithm that always produces an optimal tree for any given probabilities. While the Shannon–Fano tree is created from the root to the leaves, the Huffman

HUFFMAN CODING:

The Shannon–Fano algorithm doesn't always generate an optimal code. In 1952, David A. Huffman gave a different algorithm that always

produces an optimal tree for any given probabilities. While the Shannon–Fano tree is created from the root to the leaves, the Huffman

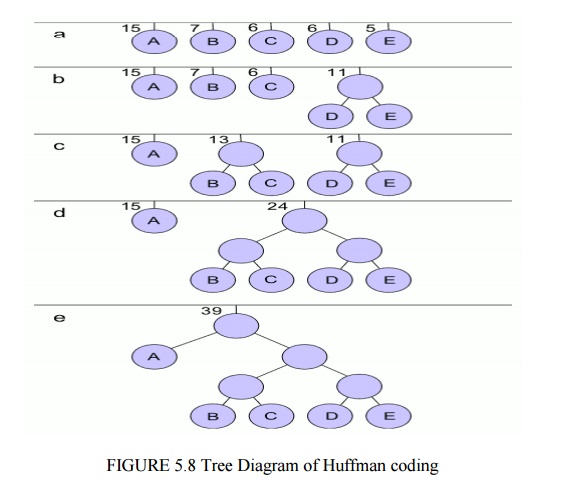
^üProcedure for Huffman Algorithm:

1. Create a leaf node for each symbol algorithm works from leaves to the root in the opposite direction and add it to frequency of occurrence.

2. While there is more than one node in the queue:

· Remove the two nodes of lowest probability or frequency from the queue

· Prepend 0 and 1 respectively to any code already assigned to these nodes

· Create a new internal node with these two nodes as children and with probability equal to the sum of the two nodes' probabilities.

· Add the new node to the queue.

3. The remaining node is the root node and the tree is complete.

^ü Tree diagram:

Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail

Communication Theory : Information Theory : Huffman Coding |