Chapter: Communication Theory : Information Theory
Channel Coding Theorem
CHANNEL CODING THEOREM:
The noisy-channel coding theorem
(sometimes Shannon's theorem), establishes that for any given degree of noise
contamination of a communication channel, it is possible to communicate
discrete data (digital information) nearly error-free up to a computable
maximum rate through the channel. This result was presented by Claude Shannon
in 1948 and was based in part on earlier work and ideas of Harry Nyquist and
Hartley. The Shannon limit or Shannon capacity of a communications channel is
the theoretical maximum information transfer rate of the channel, for a
particular noise level.
The
theorem describes the maximum possible efficiency of error-correcting methods
versus levels of noise interference and data corruption. Shannon's theorem has
wide-ranging applications in both communications and data storage. This theorem
is of foundational importance to the modern field of information theory.
Shannon only gave an outline of the proof. The first rigorous proof for the
discrete case is due to Amiel Feinstein in 1954.
The
Shannon theorem states that given a noisy channel with channel capacity C and
information transmitted at a rate R, then if R<C there exist codes that
allow the probability of error at the receiver to be made arbitrarily small.
This means that, theoretically, it is possible to transmit information nearly
without error at any rate below a limiting rate, C.
The
converse is also important. If R>C ,
an arbitrarily small probability of error is not achievable. All codes will
have a probability of error greater than a certain positive minimal level, and
this level increases as the rate increases. So, information cannot be
guaranteed to be transmitted reliably across a channel at rates beyond the
channel capacity. The theorem does not address the rare situation in which rate
and capacity are equal.
The
channel capacity C can be calculated from the physical properties of a channel;
for a band-limited channel with Gaussian noise, using the Shannon–Hartley
theorem.
For every
discrete memory less channel, the channel capacity has the following property.
For any ε > 0 and R < C, for large enough N, there exists a code of
length N and rate ≥ R and a decoding algorithm, such that the maximal
probability of block error is ≤ ε.
2. If a
probability of bit error pb is acceptable, rates up to R(pb) are achievable,
where
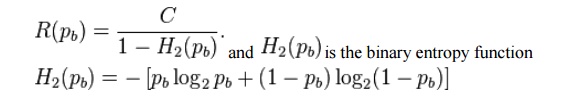
Related Topics