Solved Problems: Transient Response For DC Circuits

1. An alternating current of frequency 60Hz has a maximum value of 12A

1.     Write down value of current for instantaneous values

2.     Find the value of current after 1∕360 second

3.     Time taken to reach 9.6A for the first time.

In the above cases assume that time is reckoned as zero when current wave is passing through zero and increase in positive direction.

Solution:

Given:

F = 60Hz

Im = 12A

W = 2πf = 2π x 60 = 377 rad∕sec

(i). Equation of instantaneous value is i = Im Sin wt

i = 12 Sin 377t

(ii). t = 1∕360sec

i = 12 Sin (377∕360) = 12 Sin 1.0472 = 10.3924 A

i = 10.3924 A

(iii). i = 9.6 A

9.6 = 12 Sin 377t Sin377t = 0.8 377t = 0.9272

2. A 50 Hz, t = 2.459 x 10^-3sec alternating voltage of 150V (rms) is applied 

independently

a.     Resistance of 10Ω

b.     Inductance of 0.2H

c.      Capacitance of 50uF

Find the expression for the instantaneous current in each case. Draw the phasor diagram in each case.

Solution:

Given ,

F = 50Hz

V = 150 V

Im = Vm∕R = 212.13∕10 = 21.213

ф  = 0

For pure resistive current circuit phase different  ф 

i  = Im Sin wt = Im Sin 2πft

i  = 21.213 Sin (100 πt) A

Phasor diagram: Case (ii):

L = 0.2H

X_L = wL =2πfL X_L = 2π x 50 x0.2

X_L = 62.83 Ω

Im = Vm∕X_L = 212.13∕62.83 = 3.37A

Ф A = -90⁰ = π∕2 rad

In pure Inductive circuit, I lags V by 90 degree i= Im Sin (wt - ) A

i = 3.37 Sin Ф (wt - Ф) A

i = 3.37 Sin  (100 πt - π∕2) A

Phasor diagram

Case(iii):

C= 50uf

Xc = 1∕wC = 1∕2πfC

Xc = 1∕(2π x 50x 50 x 10^-6) = 63.66Ω

Im = Vm∕Xc = 212.13∕63.66 = 3.33 A

In pure capacitive circuit, current leads voltage by 900

= 90o = π∕2 rad

i = Im Sin (wt +ф    ) A

i = 3.33 Sin (wt +ф ) A

i = 3.33 Sin (100 πt + π∕2) A

Phasor Diagram:

3. An alternating current i= 414 Sin (2π x 50 x t) A is passed through a series circuit of a resistance of 100 ohm and an inductance of 0.31831 H. find the expression for the instantaneous values of voltage across,

a.  The resistance ,

b.  Inductance

c.  Capacitance

Solution:

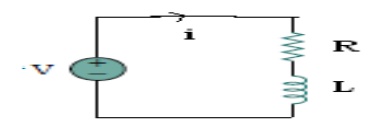
Given

i = 414 Sin (2π x 50 t) A

R = 100 Ω

L = 0.31831 H

X_L = 2π x 50 x 0.31831 = 100 Ω

(i) Voltage across Resistance:

V_R = iR = 1.414 sin (2π x 50 t) x 100

V_R = 141.4 Sin (2π x 50 t) V

(ii) Voltage across Inductance:

V_L = i X_L = 1.414 Sin (2π x 50 t + 90⁰) x 100

V_L = 141.4 Sin (2π x 50 t + 90⁰) V

4. The wave form of the voltage and current of a circuit are given by 

e= 120 Sin (314 t) 

i= 10 Sin (314 t + π∕6)

Calculate the value of resistance, capacitance which is connected in series to form the circuit. Also, Draw wave forms for current, voltage and phasor diagram. Calculate power consumed by the circuit.

Solution:

5. A resistance of 120 Ω and a capacitive reactance of 250Ω are connected in series across a AC voltage source. If a current 0.9 A is flowing in the circuit find out,

(i). Power factor

(ii). Supply voltage

(iii). Voltage across resistance and capacitance

(iv). Active power and reactive power

Solution:

Given :

R = 120Ω

6. A series circuit consisting of 25 Ω resistor, 64mH inductor and 80uF capacitor to a 110V, 50Hz, Single phase supply as shown in fig. Calculate the current, Voltage across individual element and overall p.f of the circuit. Draw a neat phasor diagram showing

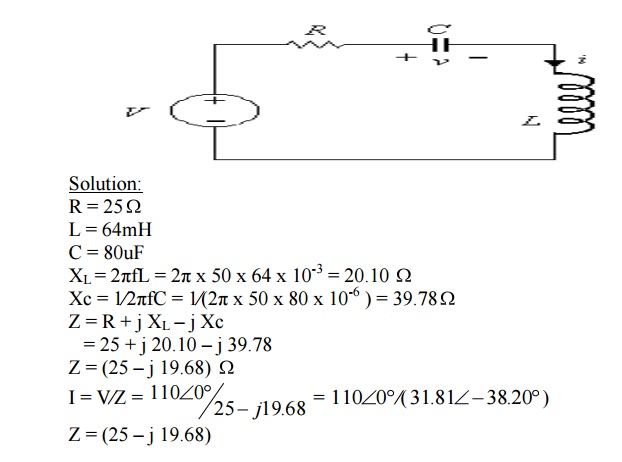
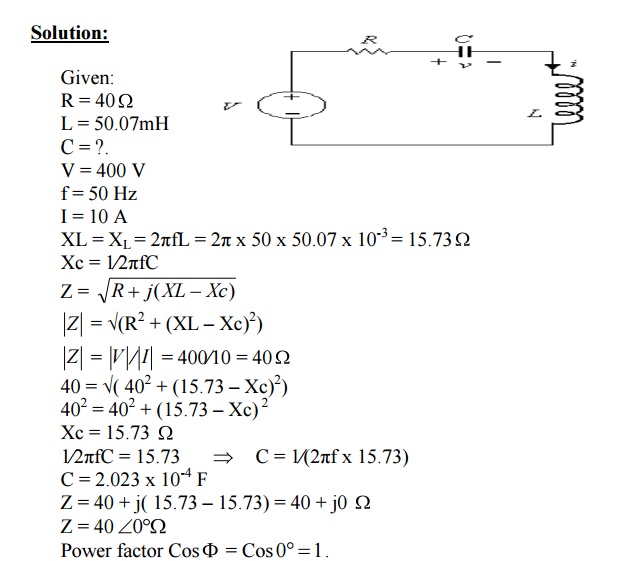
7. A series circuit having pure resistance of 40 , pure inductance of 50.07mH and a capacitance is connected across a 400V, 50Hz Ac supply. This R, L, C combination draws a current of 10A. Calculate

1.     Power factor of circuit

2.     Capacitor value

Solution: