Current lags and leads voltage in R-L series circuit

i)  Current lags voltage in R-L series circuit

ii) Current leads voltage in R-C series circuit

Solution:

Current lags voltage in R-L series circuit

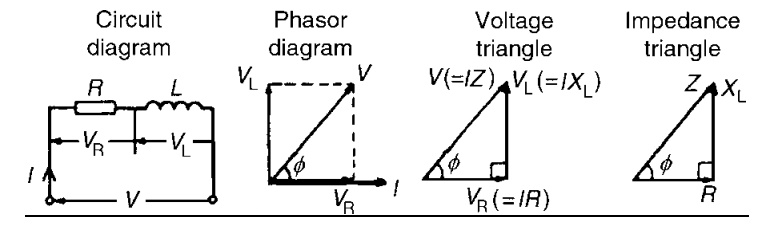
Consider a circuit consisting of pure Resistance R ohms connected in series with Inductance L henries as shown in fig.

The series combination is connected across ac supply is given by V = Vm Sinwt

The voltage drops in the circuit are,

Drop across pure resistance         V_R =  IR

Drop across pure inductance V_L = IX_L Where X_L = 2πfL

I = rms value of current drawn V_R, V_L = rms value of pure inductance

By applying KVL,

V = IR + IX _L

Steps to drawn phasor diagram:

1.  I as reference phasor

2.  R, V, I are in phase, So V_R will be along I phase in case of resistance

3.  I lags voltage by 90⁰. But I is reference, V_L must be shown leading w.r.t I by 90⁰ in case of inductance

4.  Supply voltage = Vector sum of 2 vectors V_L and V_R obtained by law of parallelogram

V = √ (V_R²) + (V_L²) = √ ((IR) ² + (IX_L) ²)

= I √ (R² + X_L²)

V = IZ

Z = √ (R² + X_L²)

From voltage triangle we can write,

Tan ф = V _L ∕V_R = X _L ∕R Cos ф= V_R∕V = R∕Z

Sin ф = V _L ∕V =X _L ∕Z

If all the sides of voltage are divided by current, we get triangle called impedance triangle.

Side or triangles are,     

1-  Resistance R   

2-  Inductive reactance X _L

3-  Impedance Z   

From this impedance triangle

R = Z Cos ф         X component of Impedance = R

X _L = Z sin ф  Y Component of Impedance = X _L

In rectangular form the impedance is denoted as,

Z = R + j X _L

While in polar form

Z = ∣Z∣∠ф Ω

Where,

∣Z∣ = √ (R² + X_L²)

ф = tan ^-1[X_L∕R]

Impedance:

Impedance is defined as opposition of circuit to flow alternating current. It is denoted by Z and the unit is ohms.

Power and power triangle:

The expression for the current in the series R-L circuit is, i = Im Sin (wt-ф) as current lags voltage

Power = V x i

= Vm Sin (wt) x Im Sin (wt-ф)

= VmIm[Sin(wt).Sin(wt-ф)]

= VmIm [ (Cosф – Cos (2wt-ф))∕2]

= (VmIm ∕2) x Cos ф - (VmIm ∕2) x Cos (2wt-ф)

Second term is cosine term whose average value over a cycle is zero.

Average power Pavg = (VmIm∕2) x Cos ф

= (Vm∕√2) x (Im∕√2) x Cos ф

P = VI Cos ф watt

The three side of triangle is,

10.VI

11.VI Cos ф

12.VI Sin ф

These three terms can be defined as below,

1. Apparent power(S):

It is defined as the product of rms value of boltage (V) and current (I). it is denoted as ‘S’.

S = VI unit is VA VA – Voltage ampere

2. Real or true power (P):

It is defined as the product of applied voltage and active component of the circuit. It is real component of the apparent power. It is measured in watts (W) or kilowatts (KW)

P = VI Cos ф  watts

3. Reactive power (Q):

It is defined as product of applied voltage and reactive component of current. It is also defined as the imaginary of apparent power is represented by Q. Unit is VAR

Q = VI Sin ф VAR

Where VAR – Volt ampere reactive.

I lead V in R-C series circuit:

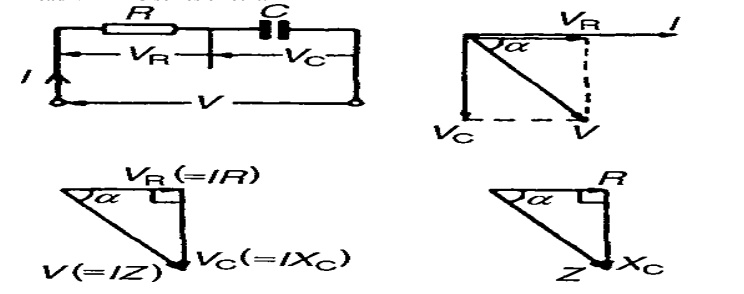
Consider a circuit in which resistance R ohms and capacitance C farads is connected across ac supply is given by,

V = Vm Sin wt

Circuit draws a current I, then there are two voltage drops,

5.     Drop across pure resistance V_R = IR

6.     Drop across pure capacitance Vc = IXc

Where, Xc = 1∕2πfC

Apply KVL we get,

V=V_R + V_C

V = IxR +IxX_C

Steps to draw phasor diagram:

^Ø    Take current as reference phasor.

^Ø    In case of resistance, voltage and current are in phase, so, V_R will along current phasor.

^Ø    In case of capacitance, current leads voltage 90⁰ i.e. voltage lags by 90⁰. so, Vc is shown downwards (i.e.) lagging current by 90⁰

^Ø    The supply voltage being vector sum of these two voltages Vc and V_R obtained by completing parallelogram

Form voltage triangle,

V = √ ((V_R²) + (Vc²)) = √(( I_R²) + (IXc²))

= I √ (R² + Xc²)

V = IZ

Z = √(R² + Xc²) is the impedance of circuit

Impedance:

Impedance is nothing but opposition of flow of alternating current. It is measured in ohms given by,

Z = √(R² + Xc²)

Where, Xc = 1∕1∕2πfC Ω called capacitive reactance.

From voltage triangle if all sides of voltage triangle are divided by current, we get impedance triangle.

The sides of triangle are R, Xc, Z

The X component is R = Z Cos ф The Y component is Xc = Z Sin ф

But direction of Xc is –Ve direction

Z = R- j Xc Ω - Rectangular form Z = ∣Z∣∠-ф Ω - Polar form

Where,

∣Z∣ =  √ (R² + Xc²)

ф =    tan ^-1[-X_c∕R]

Power and power triangle:

The I leads the V by angle ф hence, i = Im Sin (wt + ф)

Power = V x i

= Vm Sin (wt) x Im Sin (wt + ф)

= VmIm[Sin(wt).Sin(wt + ф)]

= VmIm [ (Cos(-ф) – Cos (2wt + ф))∕2]

= (VmIm ∕2) x Cos ф - (VmIm ∕2) x Cos (2wt + ф)

Second term is cosine term whose average value over a cycle is zero.

Average power Pavg = (VmIm∕2) x Cos ф

= (Vm∕√2) x (Im∕√2) x Cos ф P = VI Cos ф watts

If we multiply voltage equqtion by current I we get power equation,

1.  Apparent power (S) 

2.  Real or true power (P)       

3.  Reactive power (Q)  

Note:          

Z = R + j XL = Z = ∣Z∣∠ф Ω  ; ф is +Ve for Inductive Z

P = VI Cos ф        ;Cos ф is lagging for Inductive circuit

Z = R - j XL = Z = ∣Z∣∠-ф Ω  ; ф is -Ve for Capacitive Z

P = VI Cos ф        ;Cos ф is leading for Capacitive circuit