Chapter: Electrical and electronics : Circuit Theory : Transient Response For DC Circuits
Characterization of Two Port Networks in Terms Of Z,Y and H Parameters
CHARACTERIZATION OF TWO PORT NETWORKS IN TERMS OF Z,Y AND H PARAMETERS.
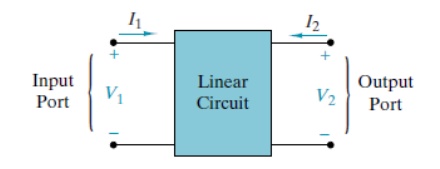
The purpose of this appendix is to study methods of characterizing and analyzing two-port networks. A port is a terminal pair where energy can be supplied or extracted. A two-port network is a four-terminal circuit in which the terminals are paired to form an input port and an output port. Figure W2–1 shows the customary way of defining the port voltages and currents. Note that the reference marks for the port variables comply with the passive sign convention.
The linear circuit connecting the two ports is
Assumed to be in the zero state and to be free of any independent sources. In other words, there is no initial energy stored in the circuit and the box in Figure W2–1 contains only resistors, capacitors, inductors, mutual inductance, and dependent sources. A four-terminal network qualifies as a two-port if the net current entering each terminal pair is zero. This means that the current exiting the lower port terminals in Figure W2–1 must be equal to the currents entering the upper terminals.
One way to meet this condition is to always connect external sources and loads between the input terminal pair or between the output terminal pair. The first task is to identify circuit parameters that characterize a two-port. In the two port approach the only available variables are the port voltages V1 and V2, and the port currents I1 and I2. A set of two-port parameters is defined by expressing two of these four-port variables in terms of the other two variables. In this appendix we study the four ways in Table W2–1.
TWO-PORT PARAMETERS

Note that each set of parameters is defined by two equations, one for each of the two dependent port variables. Each equation involves a sum of two terms, one for each of the two independent port variables. Each term involves a proportionality because the two-port is a linear circuit and superposition applies. The names given the parameters indicate their dimensions (impedance and admittance), a mixture of dimensions (hybrid), or their original application (transmission lines). With double-subscripted parameters, the first subscript indicates the port at which the dependent variable appears and the second subscript the port at which the independent variable appears.
Regardless of their dimensions, all two-port parameters are network functions. In general, the parameters are functions of the complex frequency variable and s-domain circuit analysis applies. For sinusoidalsteady-state problems, we replace s by j and use phasor circuit analysis. For purely resistive circuits, the two-port parameters are real constants and we use resistive circuit analysis. Before turning to specific parameters, it is important to specify the objectives of two-port network analysis. Briefly, these objectives are:
1. Determine two-port parameters of a given circuit.
Use two-port parameters to find port variable responses for specified input sources and output loads.
In principle, the port variable responses can be found by applying node or mesh analysis to the internal circuitry connecting the input and output ports. So why adopt the two-port point of view? Why not use straightforward circuit analysis?
There are several reasons. First, two-port parameters can be determined experimentally without resorting to circuit analysis. Second, there are applications in power systems and microwave circuits in which input and output ports are the only places that signals can be measured or observed. Finally, once two-port parameters of a circuit are known, it is relatively simple to find port variable responses for different input sources and/or different output loads.
put ports are the only places that signals can be measured or observed. Finally, once two-port parameters of a circuit are known, it is relatively simple to find port variable responses for different input sources and/or different output loads.
IMPEDANCE PARAMETERS
The impedance parameters are obtained by expressing the port voltages V1 and V2 in terms of the port currents I1 and I2.
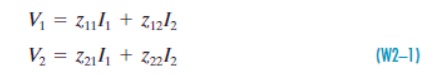
The network functions z11, z12, z21, and z22 are called the impedance parameters or simply the z-parameters. The matrix form of these equations are
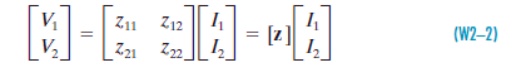
where the matrix [z] is called the impedance matrix of a two-port network. To measure or compute the impedance parameters, we apply excitation at one port and leave the other port open-circuited. When we drive port 1 with port 2 open (I2), the expressions in Eq. (W2–1) reduce to one term each, and yield the definitions of z11 and z21.

Conversely, when we drive port 2 with port 1 open (I1=0), the expressions in Eq. (W2–1) reduce to one term each that define z12and z22 as

All of these parameters are impedances with dimensions of ohms. A two-port is said to be reciprocal when the open-circuit voltage measured at one port due to a current excitation at the other port is unchanged when the measurement and excitation ports are interchanged. A two-port that fails this test is said to be nonreciprocal. Circuits containing resistors, capacitors, and inductors (including mutual inductance) are always reciprocal. Adding dependent sources to the mix usually makes the two-port nonreciprocal. If a two-port is reciprocal, then z12 z21. To prove this we apply an excitation I1 Ix at the input port and observe that Eq. (W2–1) gives the open circuit (I2) voltage at the output port as V2OC z21Ix. Reversing the excitation and observation ports, we find that an excitation I2 Ix produces an open-circuit (I1) voltage at the input port of V 1OC z12Ix. Reciprocity requires that V1OC
V2OC, which can only happen if z12 z21.
ADMITTANCE PARAMETERS
The admittance parameters are obtained by expressing the port currents I1 and I2 in terms of the port voltages V1 and V2. The resulting two-port i–v relationships are

The network functions y11, y12, y21, and y22 are called the admittance parameters or simply the y-parameters. In matrix form these equations are

where the matrix [y ] is called the admittance matrix of a two-port network. To measure or compute the admittance parameters, we apply excitation at one port and short circuit the other port. When we drive at port 1 with port 2 shorted (V2= 0), the expressions in Eq. (W2–5) reduce to one term each that define y11 and y21 as

Conversely, when we drive at port 2 with port 1 shorted (V1= 0), the expressions in Eq. (W2– 5) reduce to one term each that define y22 and y12 as

All of these network functions are admittances with dimensions of Siemens. If a two-port is reciprocal, then y12 y21. This can be proved using the same process applied to the z-parameters.
The admittance parameters express port currents in terms of port voltages, whereas the impedance parameters express the port voltages in terms of the port currents. In effect these parameters are inverses. To see this mathematically, we multiply Eq. (W2–2) by [z] 1, the inverse of the impedance matrix.
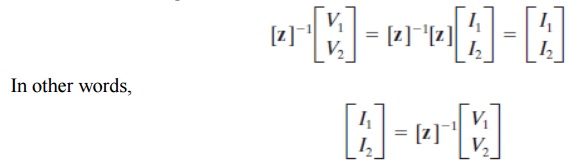
HYBRID PARAMETERS
The hybrid parameters are defined in terms of a mixture of port variables. Specifically, these parameters express V1 and I2 in terms of I1 and V2. The resulting two-port i–v relationships are
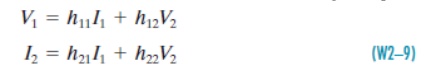
Where h11, h12, h21, and h22 are called the hybrid parameters or simply the h-parameters. In matrix form these equations are
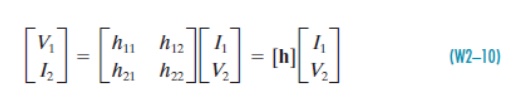
Where the matrix [h ] is called the h-matrix of a two-port network. The h-parameters can be measured or calculated as follows. When we drive at port 1 with port 2 shorted (V2= 0), the expressions in Eq. (W2–9) reduce to one term each, and yield the definitions of h11 and h21.

When we drive at port 2 with port 1 open (I1=0), the expressions in Eq. (W2–9) reduce to one term each, and yield the definitions of h12 and h22.

These network functions have a mixture of dimensions: h11 is impedance in ohms, h22 is admittance in Siemens, and h21 and h12 are dimensionless transfer functions. If a two-port is reciprocal, then h12h21. This can be proved by the same method applied to the z-parameters.
Related Topics