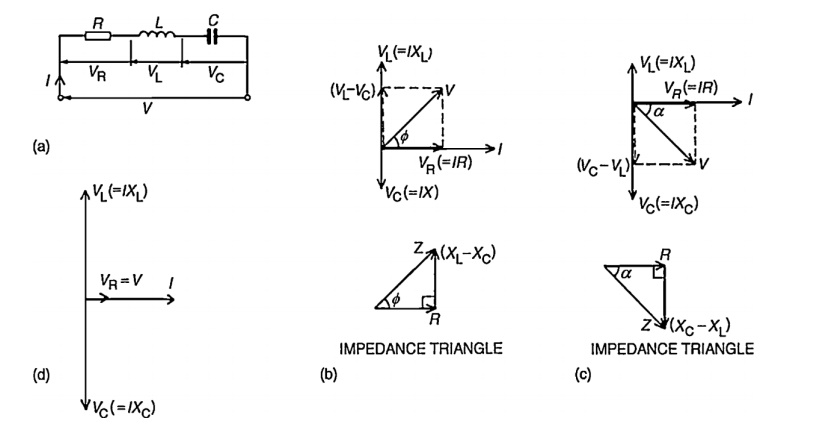
Phasor diagram for a series RLC circuit

Drawing of the phasor diagram for a series RLC circuit energized by a sinusoidal voltage showing the relative position of current, component voltage and applied voltage for the following case

a)     When X_L > Xc

 b)    When X_L < Xc

c)      When X_L = Xc.

RLC Circuit:

Consider a circuit in which R, L, and C are connected in series with each other across ac supply as shown in fig.

The ac supply is given by,

V = Vm sin wt

The circuit draws a current I. Due to that different voltage drops are,

1)     Voltage drop across Resistance R is V_R = IR

2)     Voltage drop across Inductance L is V_L = IX_L

3) Voltage drop across Capacitance C is Vc = IXc The characteristics of three drops are,

1.     V_R is in phase with current I

2.     V_L leads I by 90⁰

3.     Vc lags I by 90⁰

According to krichoff’s laws

Steps to draw phasor diagram:

1.     Take current I as reference

2.     V_R is in phase with current I

3.     V_L leads current by 90⁰

4.     Vc lags current by 90⁰

5.     obtain resultant of V_L and Vc. Both V_L and Vc are in phase opposition (180⁰ out of phase)

6.     Add that with VRby law of parallelogram to getsupply voltage.

The phasor diagram depends on the condition of magnitude of V_L and Vc which ultimately depends on values of X_L and Xc.

Let us consider different cases:

Case(i): X_L > Xc

When X _L > Xc

Also V_L > Vc (or) IX_L > IXc

So, resultant of V_L and Vc will directed towards V_L i.e. leading current I. Hence I lags V i.e. current I will lags the resultant of V_L and Vc i.e. (V_L - Vc). The circuit is said to be inductive in nature.

From voltage triangle,

V = √ (V_R² + (V_L – Vc) ²) = √ ((IR) ² + (IX_L – IXc) ²)

V = I √ (R² + (X_L – Xc) ²)

V = IZ

Z = √ (R² + (X_L - Xc) ² )

If , V = Vm Sin wt    ;  i = Im Sin (wt - ф)

i.e I lags V by angle ф

Case(ii): X_L < Xc

When X_L < Xc

Also V_L < Vc (or) IX_L < IXc

Hence the resultant of V_L and Vc will directed towards Vc i.e current is said to be capacitive in nature Form voltage triangle

i.e I lags V by angle ф

Case(iii): X_L = Xc

When X_L = Xc

Also V_L = Vc (or) IX_L = IXc

So V_L and Vc cancel each other and the resultant is zero. So V = V_R in such a case, the circuit is purely resistive in nature.

Impedance:

In general for RLC series circuit impedance is given by,

Z = R + j X

X = X_L – Xc = Total reactance of the circuit

If   XL > Xc ;         X is positive & circuit is Inductive

If   XL < Xc ;         X is negative & circuit is Capacitive

If  XL = Xc ; X =0 & circuit is purely Resistive

Tan ф = [(X_L - Xc )∕R]

Cos ф = [R∕Z]

Z = √ (R² + (X_L - Xc ) ²)

Impedance triangle:

In both cases        R = Z Cos ф

X = Z Sin ф

Power and power triangle:

The average power consumed by circuit is,

Pavg = (Average power consumed by R) + (Average power consumed by L) + (Average power consumed by C)

Pavg = Power taken by R = I²R = I(IR) = VI

V = V Cos ф

P = VI Cos ф

Thus, for any condition, X_L > Xc or X_L < Xc General power can be expressed as

P = Voltage x Component in phase with voltage

Power triangle:

S = Apparent power = I²Z = VI

P = Real or True power = VI Cos ф = Active power

Q = Reactive power = VI Sin ф