Small Circular Holes in Plates, Tunnels, and Inclusions

Small Circular Holes in Plates, Tunnels, and Inclusions

Small holes are often cast or drilled in plates for everything from conduits to windows. Corresponding situations in plane strain are tunnels or shafts. A related question is the inclusion problem where the hole is filled with a mate-rial of different stiffness than the plate. Rather than the normal and shear stresses disappearing on the hole boundary, displacement conditions can be specified. The practical design situation of lined holes falls between the two extremes of an unreinforced hole and a rigid inclusion.

Solutions for circular holes and inclusions are relatively straightforward in polar coordinates if the external boundary is distant enough so that the per-turbation from the hole essentially damps out by St. Venant’s principle into the free field and the boundaries do not interact. This will be the assumption in this section. For noncircular holes or when the hole and external boundary interact, the problem usually requires either conformal mapping with com-plex calculus, experimental analysis, or numerical solution. We shall see, however, that, in certain optimum design cases such as harmonic or neutral holes, some or all of these restraints on geometry disappear.

Isotropic Field

Lamé’s solution for external pressure can be used directly for a small circular hole in an isotropic free field (i.e., Mohr’s Circle is everywhere a point). If, as in Figure 7.2 we assume b > a, then for uniform tension, σ_m, on the external boundary, the stress function is:

Thus the effect of the hole is to introduce purely deviatoric stress and there is no perturbation of the original isotropic field. In other words, everywhere:

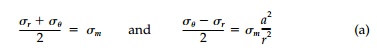
The hole’s effect is entirely captured in the first term of the stress function which is, itself, harmonic. This remarkable result, as plotted in Figure 7.2, leads directly to the design criterion for harmonic holes. That is, a harmonic hole shape is that which does not perturb (anywhere) the isotropic compo-nent of the stress field into which it is placed and, therefore, introduces only deviatoric stresses everywhere.

The stresses damp out parabolically as r². For example, at r = 5a the differ-ence from the original field (i.e., zero) is 4%. At the hole boundary, r = a:

Example 7.2

A thick brass ring (b = 2a) with internal pressure p = 6000 psi is enclosed by a rigid boundary as shown below. Assume 12,000 psi.

(a)        Determine the stress field and plot.

(b) What is the factor of safety against yield?

To get ahead of ourselves, it is clear from comparing solutions for a hole and for a rigid inclusion, that there must be some happy intermediate case where the hole boundary is reinforced (stiffened) in such a way that there is no change in the field stresses whatsoever. This is an optimum design that is truly optimum in that the plate will never know there is even a hole in it. 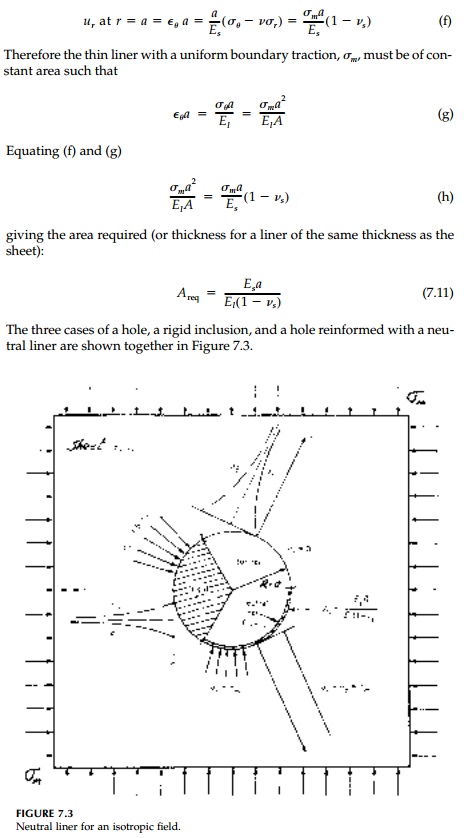Both the isotropic and deviatoric components are unperturbed and there is no stress concentration.

We will call this absolute optimum a neutral hole.* In plane stress the reinforce-ment can be provided by thickening the sheet near the boundary or by using a liner of stiffer material. The second option is the only feasible one for plane strain.

The shape of the neutral hole in an isotropic field is certainly circular and, if we assume a liner with El>> E_s, then it will be “thin”. The contact stress must be σ_m and the interface must move radially the same as the uncut sheet at r =  a. That is:

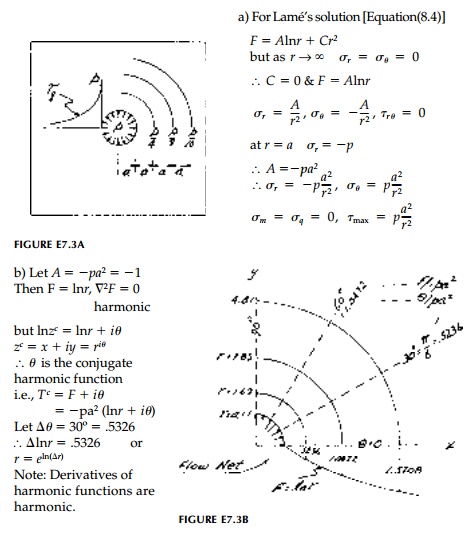
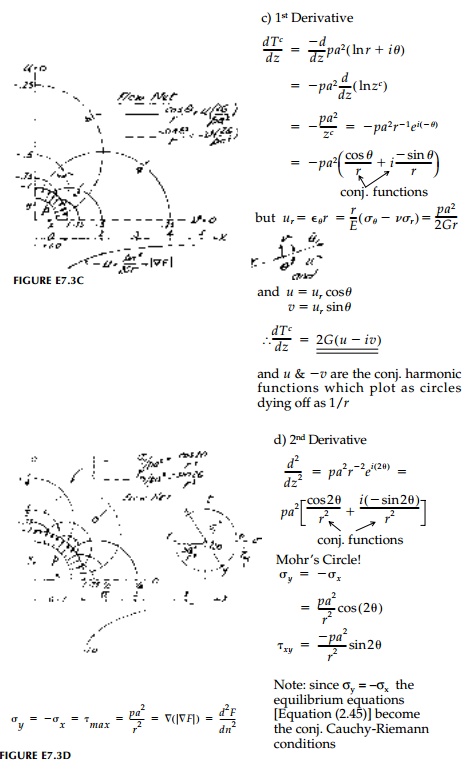
Example 7.3

Derive the solution (stress field) for uniform pressure, p, applied to a small hole (radius = a) in a large plate.

a.  Plot contours of σ_q,τ_q.

b.  Is the stress function harmonic? If so determine its conjugate and plot the flow net.

c.  Determine the displacement field in Cartesian coordinates and plot contours of u and v. Discuss.

d. Derive at least one more set of conjugate harmonic functions and plot. (Hint: Consider the equilibrium equations in Cartesian coor-dinates.)

Deviatoric Field

A purely deviatoric field, where there is no isotropic component, can be thought of as pure shear at 45� o from the principal orientation. For the sheet without a hole, the deviatoric, free-field stress function is

If we now drill a small circular hole as in Figure 7.4, the perturbation must rapidly damp to this free field and thus a stress function of type II is required with m = 2. However, the first term in the general form:

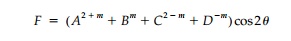
can be eliminated since stresses would increase as r². Therefore, assume

Although the stress concentration is twice that for the isotropic case it is, as shown in Figure 7.4, much more localized.

General Biaxial Field

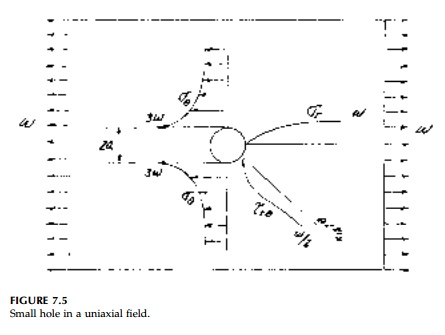
By superimposing isotropic and deviatoric components in differing ratios, the stress distribution introduced by a small hole in any biaxial field can be obtained. The particular case of uniaxial tension, w, is shown in Figure 7.5. Setting σ_m = σ_d  = w/2 the Kirsch solution for the stress field is

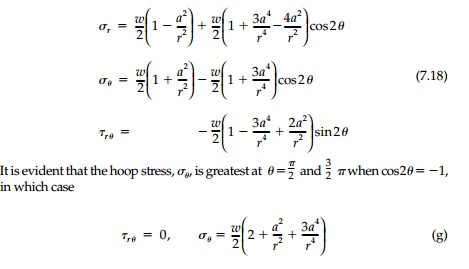
again dying away rapidly from the hole boundary, although not quite as quickly as for the deviatoric free field.