Lame’s Solution for Rings under Pressure

Lamé’s Solution for Rings under Pressure

A pressurized cylindrical ring might have been discussed in previews pages since the field equations can be integrated directly. However, since it and derivative solutions are so elegant, practical, and intriguing because of their optimal properties, this simple case has been reserved as an introduction to this chapter devoted to this general class of structures.

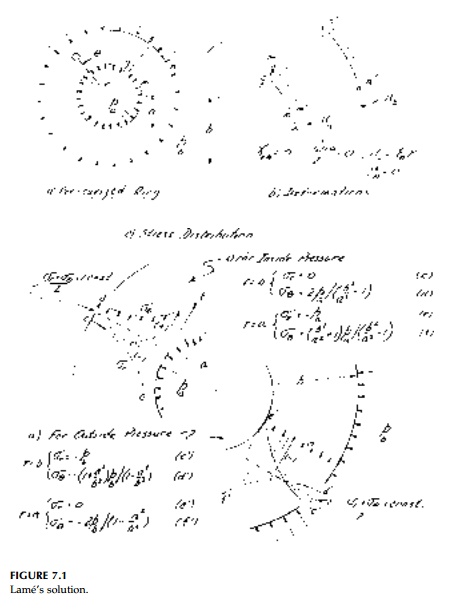
Consider a thick ring as shown in Figure 7.1a of outer radius, b, and inner radius, a, subjected to uniform internal and external pressures p_a and p_b. This might be a transverse section in generalized plane strain cut from a cylinder away from the ends. From symmetry, each radial line (longitudinal section) must simply move radially along its original position the same as any adja-cent radial line (Figure 7.1b). Therefore, nothing can be a function of Î¸ and there is no shear strain (or stress) or elastic rotation.

Thus the equilibrium equations reduce to a single requirement:

and from the conjugate relationship between the first invariant and elastic rotation [Equation (5.13)]

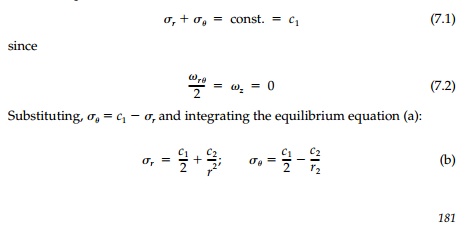
This stress distribution for internal and external pressure considered sepa-rately is plotted in Figure 7.1c.

The solution by the stress function approach is equally straightforward. Since nothing can be a function of Î¸, the stress function must be of type I.

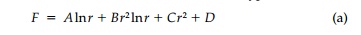
We have seen, when considering the pure bending of a ring, that the B term contributes to the displacements by introducing [Equation (6.28)] an elastic rotation  Ï‰_z= 4Bθ/E   which is not single-valued and therefore not possible for complete rings. Therefore, taking B as zero, the stresses are:

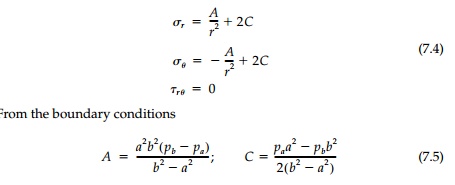
giving the same solution for the stress field [Equation (7.3)].

Since there are no shears or rotation, all points move radially outward and

Clearly this Lamé solution* leads to many practical applications. For thin rings b - a = t << r, the strength-of-materials approximation: Ïƒ_r =0 (assumed) ÏƒÎ¸ = (p_a - p_b)r/t is adequate for design. For thick-walled rings, the advantages of prestressing to apply p_b to reduce the inner tensile hoop stress produced by internal pressure p_a is obvious. A number of examples are given as chapter problems.

Example 7.1

A thick, oval, cylindrical pressure vessel has the cross-sectional dimensions shown below. Assume plane stress. By superpoisition of elasticity solutions, determine the maximum stress and the yield pressure.

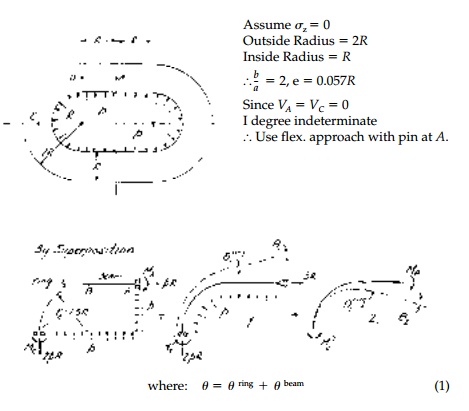
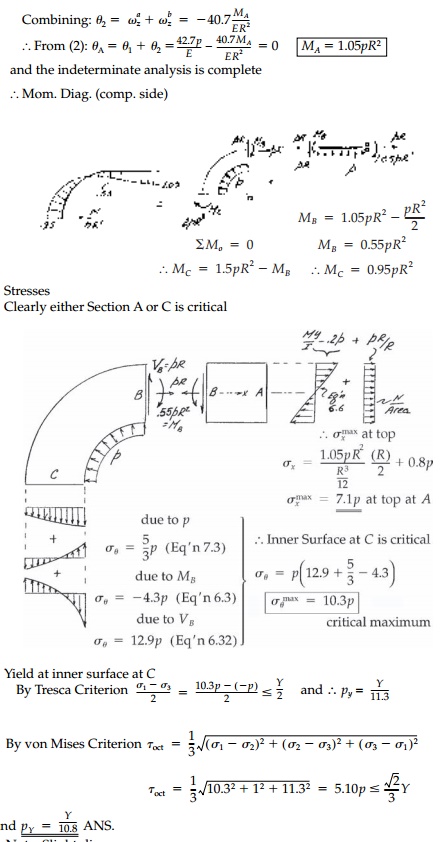
Note: Slight discrepancy at B where the neutral axis of the beam is at the centroid and of the ring at  - e =  - .057R. However, this section is not critical and resulting error at C is, by St. Venant’s principle, negligible.