Harmonic Holes for Biaxial Fields

Harmonic Holes for Biaxial Fields

Since the biaxial field is so commonly encountered in structural mechanics, it is selected first to illustrate the application of the general functional equation. In addition, a uniformly distributed normal traction of magnitude P (positive if tension) applied to the unknown hole boundary is also included. Thus the boundary loading function is

where P is zero for the unloaded hole.

For the plane problem, consider the biaxial free field specified by the prin-cipal stresses N1, N2, which have constant magnitude and direction at every point in the plane and where it will always be assumed that the direction of N1 coincides with the x-axis and that |N1| >= |N2|. For these conditions

Finally, substituting these expressions into the general integral equation and combining similar terms, one obtains

Substituting, the coefficient a1 can be expressed in terms of the principal stresses as

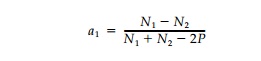
Thus the mapping function whose boundary value describes the geometry of the harmonic hole for a biaxial field with uniform boundary loading is

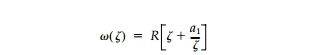
In the z-plane the boundary value of this mapping function describes an elliptic hole with major axis, a, oriented parallel to the direction of the major prin-cipal stress N1, and where the ratio of the major to minor axes of the ellipse is

Harmonic holes with stresses along the x-axis for a particular biaxial field are shown in Figure 7.7a.

Conditions to ensure the existence of a harmonic hole shape in a biaxial field correspond to a breakdown in the conformality of () which, in turn, coincide with physical conditions on the original stress field. Considering the first derivative of the mapping function on the boundary,

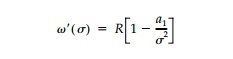
the conformality of ω(σ) breaks down when a1 =   +- 1. However, if the direction of N1 is to be parallel with the direction of the major axis of the ellipse, as has been specified, a1 can only vary between 0 and + 1. Obviously, if a1  = 0, a cir-cular hole is the harmonic shape; and this occurs when N1=N2 regardless of the value of P. For a1 =+ 1, the harmonic hole is a slit parallel to the direction of N1. In the case of an unloaded hole (i.e., P = 0), the limitations on the values for the coefficient a1, establish the following limitation on the field:

This relationship is satisfied only if N1 and N2 have the same sign (i.e., both tension or both compression). In the case of a uniformly loaded hole

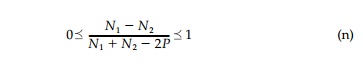
This relationship is satisfied when N1 is positive (i.e., tension) only if N2 <=P and when N1 is negative (i.e., compression) only if N2  P. It is helpful to note that these limitations on the type of biaxial field for which a harmonic hole exists may be more easily visualized by realizing that the ratio a/b in Equation (7.25) must always be greater than or equal to one.

At the other extreme of a rigid inclusion, the harmonic shape can be found from Equation (7.23b) following an analogous procedure. Substituting, Equation (7.24) becomes

Thus, the rigid harmonic inclusion is an ellipse of arbitrary size with the ratio of major to minor axes:

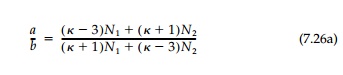
or, in terms of principal normal strains, simply

the variable a coinciding with the x-axis. In an isotropic field where N1=N2 the shape, as expected, is a circle.

The stresses on the boundary of any rigid inclusion are

As can be seen, harmonic inclusions not only give the required condition  σθ = N1 + N2 at the interface, but also no shears so that, in fact, the contact stresses are principal with no tendency for slip to occur at the interface.

To demonstrate these results, the same test case N1 = 2N2 = 4P with v =1/4 is shown in Figure 7.7b for both plane stress and plane strain. Both harmonic holes and harmonic inclusions are ellipses oriented with the principal stresses but in opposite directions. The unloaded harmonic hole has a ratio of the axes proportional to the ratio of the original principal stresses while this ratio for the elliptic harmonic inclusion is inversely proportional to the original princi-pal strains (irrespective of the planar condition).

For the rigid inclusion, the condition for existence is similar to that for holes in that a/b > 0 and therefore it can exist only when

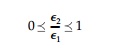
It is clear that holes that are harmonic must produce minimum stress concen-tration in constant fields since maximums and minimums in Laplacian fields must occur on the boundary. It can now be shown that the same is true for a rigid harmonic inclusion. For example, in plane stress the in-plane normal strains are given by:

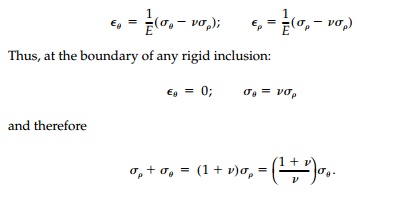
But the minimum value possible for the first invariant in a constant field is simply N1+ N2 so the minimum stresses possible on the boundary are:

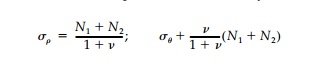
which are in fact, those for the harmonic inclusion [Equation (7.27)]. The proof for plane strain is similar. Although the standard uniqueness theorems of elasticity do not apply directly to the “inverse problem,” it is hard to con-ceive of other shapes that might fulfill the harmonic design requirement for a given original stress field since this would be comparable to finding two different shapes that have precisely the same value of stress or displacement at every point on the boundary. Again comparing the two “extreme” alterna-tives of holes and rigid inclusions, it seems, from Figure 7.7 that a rigid inclu-sion is somewhat closer than an unloaded hole to the absolute optimum of a neutral hole with no stress concentration whatsoever. Comparing each har-monic shape for the test case N1 = 2N2, = 1/4, to the corresponding circular shape, the stress concentration factor is reduced from 2.5 to 1.5 for an unloaded hole and from 1.56 to 1.2 for a rigid inclusion in plane stress. In either case, the practical benefits that accrue from using harmonic shapes are important.