Chapter: Civil : Principles of Solid Mechanics : Rings, Holes, and Inverse Problems
Harmonic Holes and the Inverse Problem
Harmonic Holes
and the Inverse Problem
Large stress
concentrations at the edges of holes produce serious structural problems.
Overstressed areas, no matter how local, often lead to fatigue cracks greatly
reducing the life of a structure or even triggering collapse if they are not
detected or if they propagate rapidly.
However, two design
modifications may be beneficial. The shape of the hole might be changed and/or
the hole boundary reinforced by thickening the plate locally or providing a
liner of stiffer material. Such an inverse approach, where the geometry of the
boundary is left as an unknown, might be called ŌĆ£shape mechanics.ŌĆØ It involves
a fundamental reorientation of solid mechan-ics to thinking about design
conditions and optimum shapes to control fields rather than accept
unsatisfactory fields dictated by prescribed geometry.
The search for optimum structural
shapes has traditionally been conducted by engineers using a strategy
distinctly different from that of standard math-ematical analysis where the
governing equations are solved for a given set of boundary conditions on a body
of specified geometry. Instead, the engineer leaves at least some geometric
parameters unspecified but imposes extra con-ditions on the stressŌĆ'strain field
sufficient to then derive a configuration ŌĆ£optimizedŌĆØ to that preselected
design criterion.
Linear and shell
structures provide a classic example of this alternative design strategy in
which the search for optimum shapes to eliminate bending and the resulting
effects on building forms is a major historical theme. In startling con-trast,
there is essentially no counterpart to the design tradition in elasticity. A
200-year history has produced a rich and elegant mathematical theory in both
real and complex representation but, thus far, the inverse approach has
generally been bypassed. There are a number of historic and philosophic
influences one might postulate to explain, at least in part, this obvious
omission but probably the most important factor is the lack of clear design
criteria for inverse elasticity that can be translated into precise
mathematical statements comparable in power and scope to the no-bending or
minimum energy condition in structures.*
Design Condition
The choice of design
condition is absolutely crucial to the inverse strategy in that it dictates all
that follows. The engineer should logically look for a powerful design
condition that can be translated into a precise mathematical statement
independent of coordinate systems and incorporating the fundamental proper-ties
of the final stressŌĆ'strain field everywhere, not just at the unknown boundary.
We have seen that the
circular shape for holes or rigid inclusions are opti-mum giving minimum stress
concentration, but only for an isotropic field. In this case, not only are the
boundary stresses constant and their sum equal to
twice the isotropic
stress (i.e., the value of the first invariant) but, quite remarkably, this is
also true everywhere in the resulting field as the perturba-tions of the
individual stress components damp out. With the circular shape as a model, let
us therefore choose for the design criterion the ŌĆ£harmonic field conditionŌĆØ
that, when the hole or inclusion is introduced, the first invariant of the
stress (or strain) remain unperturbed everywhere in the field. The shape of the
new boundary that achieves this is, in turn, called a ŌĆ£harmonic shape.ŌĆØ
This name is used for
obvious reasons. If, in any portion of an uncut two-dimensional domain in plane
stress or plane strain defined by a known ŌĆ£originalŌĆØ stress function F┬ o ,
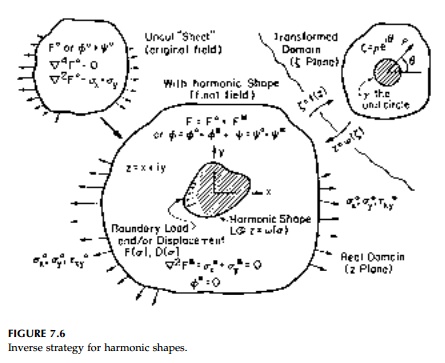
a new boundary is introduced, such as the hole in Figure 7.6, then the final
field, F, is given by

The superscript o
indicates an original quantity before a harmonic shape is introduced, and the
superscript * indicates the change or perturbation of this quantity due to the
new harmonic boundary. The final state, being always the sum of these two
components, is given no superscript.
Because the ŌĆ£perturbation stress functionŌĆØ, F*, is harmonic, so must all changes in all stress, Žāij*, , strain, Eij*, and displacement, uij*, components when the unknown boundary is introduced. For example, the equilibrium equa-tions for the perturbation:
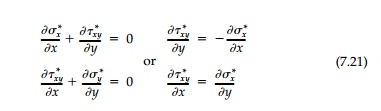
become the
Cauchy-Riemann conditions since Žāx* = - Žāy*.
Therefore, the normal and shear components of the induced stresses and strains
are actually conjugate harmonic functions. Similarly, because there is no
change in the first invariant, there can be no elastic rotations and
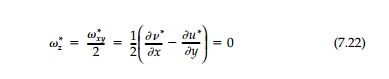
Since Ex* = - E y*, u* and -v* must be conjugate harmonic function as well. Thus, the analogy between the harmonic design condition and the mem- brane shapes for arches and shells is complete. For membrane structures the ŌĆ£no bendingŌĆØ condition is actually, of course, a requirement that there be no elastic rotations of any cross-section and the harmonic condition gives a full two-dimensional counterpart imposing ŌĆ£no bendingŌĆØ anywhere in the field when the harmonic shape is introduced.* Thus, as engineers, we might expect, with the benefit of historical perspective, optimum behavior from designs fulfilling the harmonic condition.
Harmonic shapes can be
derived in a number of ways. It is, after all, only the perturbation, F*,which
is sought and, by imposing the harmonic condi tion, the biharmonic field has
been reduced to the simplest elliptic form. It can also be shown that both F*
and its normal derivative can be completely specified on the unknown boundary
in terms of F┬ o . Essentially then, the prob-lem becomes directly
analogous to the classic question of determining the shape of a free-surface in
Laplacian fields and all the experimental, numeri-cal, and mathematical
techniques employed in the various disciplines where this problem arises might
conceivably be used.*
Since we seek the geometry of an unknown boundary, a complex variable formulation such as presented by Muschelishvili** offers a particularly pow-erful analytic approach. As shown in Figure 7.6 , we can describe an opening of essentially any shape as a function of the complex variable z = x + iy, and it becomes convenient to map from a region containing a circular opening using the inverse transformation z = Žē (╬Č) . Stresses, strains, and displace-ments for the plane problem without body forces can be expressed in terms of two complex functions ŽĢ(╬Č) and ╬©(╬Č) which, in the standard problems of elasticity, are determined from the boundary condition:
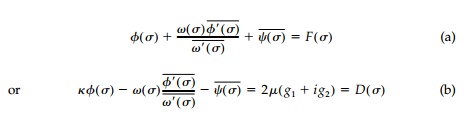
in which Žā(without a subscript) equals the value of ╬Č on the boundary of the unit circle ╬│. The first of these
equations is for the first fundamental problem of elasticity in which F(Žā)
represents any self-equilibrating boundary loading, while the second is for the
second fundamental problem in which g1 and g2
are
the known boundary
values of any displacement components u and v imposed on ╬│.
The material properties k and 2╬╝ may also be written:
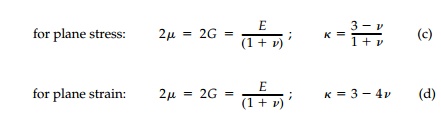
in terms of YoungŌĆÖs modulus, E, and PoissonŌĆÖs
ratio, v.
For standard analysis
where geometry is known, the problem becomes the determination of the complex
potentials ŽĢ and ╬©.
For the inverse problem on the other hand, the desired shape will be given
directly by the unknown mapping function Žē(Žā),
which can be found from the applicable boundary condition only if the unknown
perturbation components ŽĢ* and ╬©*
can be eliminated. The har-monic condition allows us to do this since it
requires that:
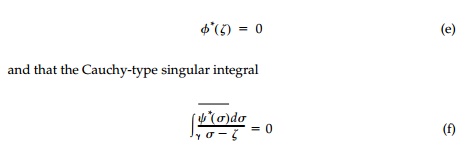
Thus, multiplying each term in Equations (a) and (b) by dŽā/(Žā- ╬Č) and inte-grating over the boundary, the basic equations for the form of the harmonic shape (opening or inclusion) are found to be:
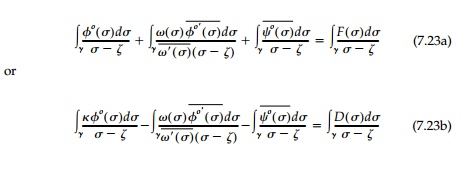
Related Topics