Neutral Holes

Neutral Holes

For both unlined holes and rigid inclusions, it is possible to leave the geom-etry of an opening unspecified thus inverting the standard problem in elas-ticity to solve for shapes to achieve an optimum design specification on the final stress state. The design criterion that has been used so far, the har-monic field condition, specifies that the first invariant of the stress tensor, satisfying Laplace’s equation, remain everywhere unperturbed when the shape with unknown boundary loading or displacements is introduced. Such shapes for holes or inclusions, termed “harmonic shapes,” apparently produce the minimum stress concentration possible in any given free field. These are, therefore, optimum for the cases where there is either no liner or the liner is rigid.

Between the two extremes of no liner or a rigid hole interface, it may be possible to find a flexible liner designed such that all perturbation of the field is eliminated. In this case using the same inverse strategy, not only is the shape unknown, but so are the stiffness properties of the liner. However, in this case as recompense for the added unknowns, both the deviatoric and iso-tropic components of the stress and strain and all displacements are known everywhere since they are the same as the uncut sheet.

The combination of hole shape and liner stiffness to give complete field restoration through structural equivalency is a special subset of harmonic shape called a “neutral hole” by Mansfield. He was the first to clearly define

this inverse problem and develop a theory for the special case of membrane reinforcement. A more general theory, with examples where flexural as well as axial stiffness of the liner is included, should be of immediate practical consideration for new design in almost every area of structural mechanics where eliminating all stress concentration will lead to less material.*

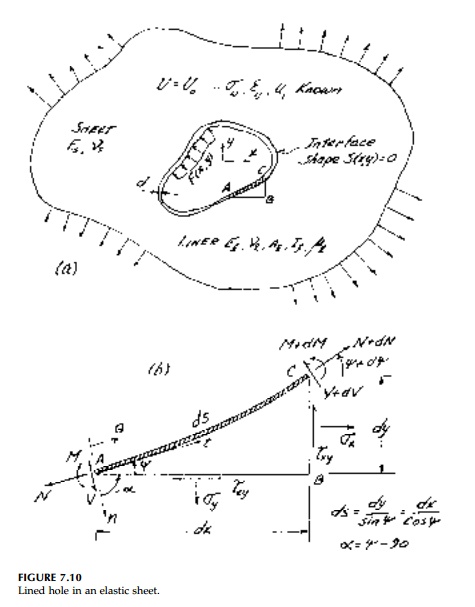
The parameters of the problem are shown in Figure 7.10. Making the “sim-plest” assumptions of two-dimensional elasticity theory without body forces, the inverted problem for the neutral hole can be stated as shown in Table 7.1

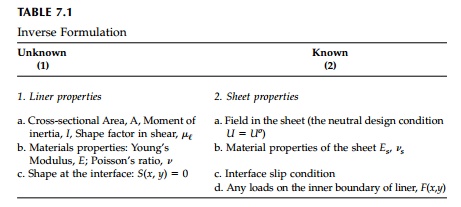
where the symbol U is used for the stress function rather than F so as not to confuse it with the boundary loading.

The properties of the liner required to achieve the neutral condition will of course depend on all the “known” variables. Let us confine ourselves here to a straightforward but realistic and powerful specification of these variables.

1.  Field stresses (and, therefore, strains and displacements) will remain unperturbed in every respect (i.e., the liner will behave exactly as the material did in the cavity into which the liner is placed).

2.  Only the general biaxial and linear gradient free fields will be considered.

3.  Material properties are constant and the modulus ratio, E_l/E_s, is such that the liner can be considered a “thin” ring (i.e., radius to thickness ratio R/d > 10).

4.  A no slip condition exists at the interface.

5.  The inner surface of the liner is not loaded [i.e., F(x,y) = 0].

Within this framework, the problem may be “underspecified” for a unique solution emphasizing the “design” nature of this approach.

Generalizing Mansfield’s derivation to include flexural stiffness, consider first the equilibrium of the diferential element of the liner shown in Figure 7.10b:

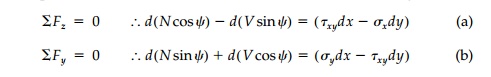
However, since the right hand side of Equations (a) and (b) are total differen-tials in terms of the stress function, U, they can be integrated to give:

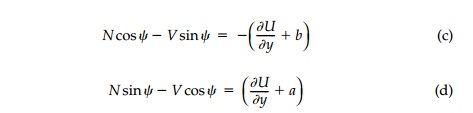
in which (a) and (b) are arbitrary constants. Solving for the normal and shear force resultants separately:

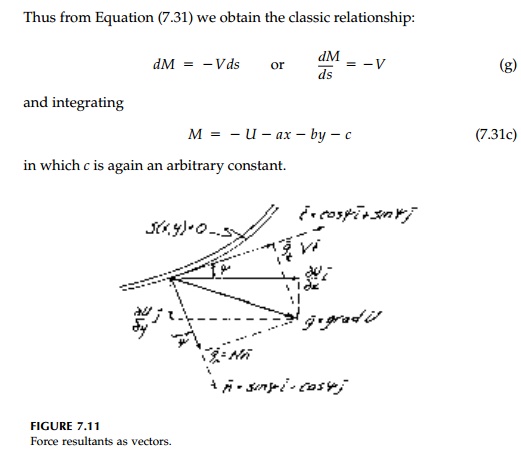
Thus, with Equations (7.31), the internal force resultants and moment can be determined for the liner for a prescribed shape in any given field, U, inde-pendent of material properties. Since terms such as ax, by, and c can be added to U without affecting stresses in the sheet, they can be used to adjust the V, N, and M diagrams or the position and size of the hole. For the case of a neu-tral membrane liner without flexural stiffness, Mansfield’s equation for the neutral shape is obtained directly from Equation (7.31c) as

if the arbitrary constants are neglected.

These basic equilibrium equations can also be considered in terms of vector components as shown in Figure 7.11 where t and n are unit tangent and nor-mal vectors. If we neglect the arbitrary constants a, b, and c, and define the vector g = Pi + Qj = grad U, the internal force equilibrium conditions are simply that N and V are the magnitudes of the normal and tangential compo-nents of the directional derivative of U. That is

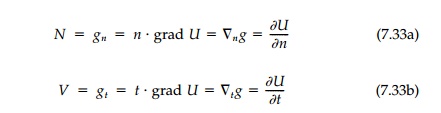
If for membrane reinforcement the moment is zero, then the shear must be zero and the neutral shape is a level line of U.

It should be emphasized that equilibrium Equations (7.31) apply in gen-eral to any liner or, for that matter, all problems involving a flexible member interacting with an elastic medium. As such they are quite remarkable in that they give a physical interpretation of the stress function and its gradient at the interface. However, only for the inverse problem where U is known

(or perhaps for the standard problem if the moment and force resultants were measured experimentally) is it possible to use them directly.*

Displacements of the liner and strains at its neutral axis due to the internal moment and force resultants can now be found by the so-called “generalized equations of Bresse.”** The cross-section will be displaced and will rotate as shown positively in Figure 7.12a. Considering a differential length, assuming plane sections, and neglecting any contribution from the normal expansion or contraction of the liner, then in curvalinear coordinates:

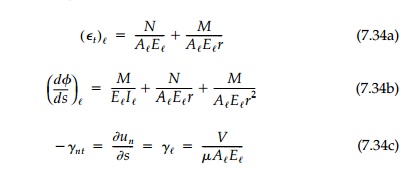
in which the final equation includes only the contribution to u_n due to shear “warping.” To obtain the displacements of the liner, these equations must be integrated along its length in the usual fashion.

Finally for the sheet, the strain components, (E _ij)_s, can be obtained directly from the stresses which, in turn, can be converted to stress-function relationships by the standard definition and transformation. Doing this for only those compo-nents necessary for the compatibility match:

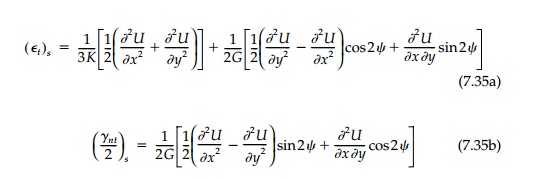
The rotation of the sheet at the interface, as shown in Figure 7.12b, is given directly by

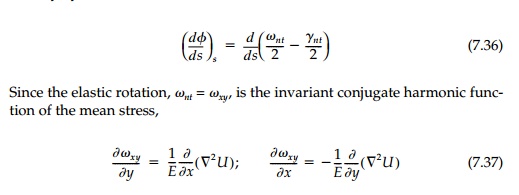
the relative rotation of the interface [by Equation (7.19)] can also be expressed in terms of the stress function. Displacements of the sheet, (u_i)_s, can be found by integrating the strains directly.