Harmonic Holes for Gradient Fields

Harmonic Holes for Gradient Fields

Using the complex-variable representation of the plane theory of elasticity, it has been possible to invert the standard problems of classical elasticity to solve for the geometry of a hole that does not anywhere perturb the first invariant of the original free field. This design criterion and the resulting shapes are termed “harmonic” not only because the first invariant, which is harmonic, remains everywhere unchanged, but also because all perturba-tions of the original stress�'strain field are harmonic as well. For a constant field the harmonic ellipse does produce constant boundary stresses and a minimum stress concentration and it is postulated that such harmonic shapes are, in fact, “optimum” in that they produce minimum stress concentrations in any field for which they exist.

In theory at least, the harmonic field condition, Equation (7.20), and the resulting boundary integral Equations (7.23) apply to any field. The only unknown in these equations is the harmonic hole geometry ω(σ), which is the boundary value of the conformal mapping z = ω(ζ) from the exterior |ζ| =1 of the unit circle in the ζ- plane. The complex potentials ϕ0(σ) and Ψ(σ), which define the original free field, and F(σ) and D(σ), which describe the boundary loading or deflection are always known functions of ω(σ). In these terms, σ (no subscript) is the value of ξ =p eiθ on the boundary of the unit cir-cular hole γ with center at the origin (i.e., σ = eiθ).

A solution of this equation for  ω(σ) therefore determines the harmonic hole shape. In addition, it should be reemphasized that the equation admits great generality in that one may obtain solutions for either constant or nonconstant fields with either constant or nonconstant boundary loads.

Consider the simple case of a linear gradient field (e.g., bending) acting within a region large in comparison with the size of a hole to be cut. Super-imposing on this field an isotropic field, the resulting components of the com-bined field in the absence of a hole are

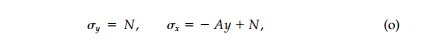
where A is a real constant that determines the slope of the linear field and N is the magnitude of the isotropic field component. The fact that this stress field is unbounded at infinity causes no particular difficulty since one need only consider a sufficiently large finite region in which all stresses are bounded.

For this combined field with a uniform pressure “P” (positive if tension) on the hole boundary:

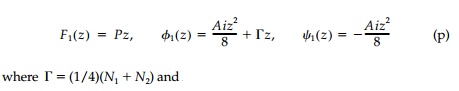
N1, N2 are the principal stresses. Transforming these equations to the ξ-plane they become

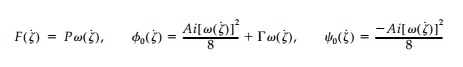
Finally, substituting the foregoing expressions into the harmonic hole equa-tion and combining terms one obtains as the functional equation to be solved for ω(σ):

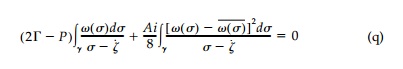
It is important to note that unlike integral equations encountered in the solution of the standard elasticity problem where the mapping function is known, Equation (q) expresses the condition that must be satisfied by the boundary value of the unknown mapping function. Since it is the boundary value of the final mapping function that must satisfy Equation (q), it is only necessary that functional representation of ω(σ) be shown as a gen-eral rational polynomial containing both negative and positive powers of

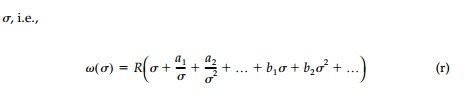
In this equation R is a real scaling constant and the a’s and b’s are complex constants. As can be seen, such an expression allows a far more concise representation of the hole geometry than could be obtained if the positive powers of  σ >2 were omitted and, in fact, if these positive powers of σ are not included, a closed-form polynomial solution cannot be obtained.

Substituting Equation (r) into Equation (q) and evaluating, one can show that a solution exists when

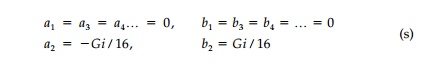
Here, G is a nondimensional parameter called the “gradient field strength,” which relates the relative strength of the original field components (A,�'), the half depth of the hole (R), and the boundary loading

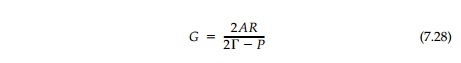
In the present case of a gradient superimposed on an isotropic field, G = 2AR/(N - P). Thus the boundary value of the mapping function that describes the shape of the harmonic hole for an isotropic field with superimposed linear gradient and uniform boundary loading is

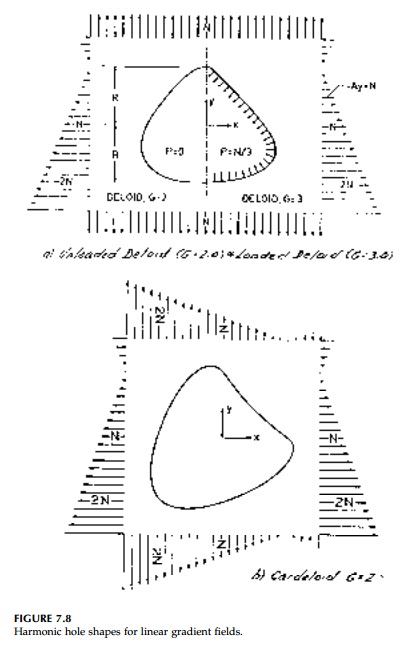
This harmonic hole shape is called the “deloid.” When the point σ in Equation (t) describes the unit circle γ, the point (x, y) describes the deloid in the z-plane the parametric representation of which is

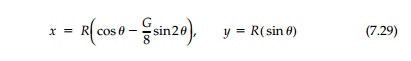
The geometry of a deloid with an unloaded boundary for an original stress field of G = 2.0 and a deloid in the same original stress field, but with a uni-form boundary loading that results in a G = 3.0 is shown in Figure 7.8a.

Following the same procedure for a stress field where both principal stresses vary linearly, the “cardeloid” can be obtained with the parametric representation:

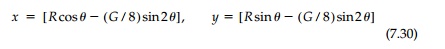
Using Equation (t) the range of values of G for which ω(σ) presents a con-formal transformation can be obtained. This range is the same for both the deloid and cardeloid and is simply |G|<4.0. In the case of the unloaded hole (i.e., P = 0) this condition establishes the following limitation on the stress field and hole size:

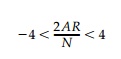
which is physically satisfied only if the entire hole boundary occupies a region in the original stress field where the first invariant (or mean stress) has the same sign.

While it has been postulated that harmonic holes are also optimum in that they produce minimum values of stress concentration for any hole shape in any free field for which they exist, this postulate has only been proven for the constant free-field. Nonetheless one can obtain an idea of the extent to which harmonic holes can reduce stress concentrations in nonconstant fields by com-paring the stresses on the boundary of an unloaded harmonic hole to those for a circular hole most commonly encountered in practice.

For example, Figure 7.9 shows the boundary values of the tangential normal stress τθ nondimensionalized by the isotropic field stress N, for the deloid G= 3.0 and a circular hole of the same size in the same position. It is clear that the

deloid has not only significantly reduced the maximum stress, but it has also significantly reduced the total variation of stress around the hole boundary.

In the next two sections we will go on to the question of the neutral hole where both the shape and the properties of reinforcement to eliminate all stress concentration are presented for the same simple free fields discussed here for unlined harmonic holes. However, the essence of inverting elastic analysis to a design orientation should not be lost in the details of a particular solution. Since the inverse problem in elasticity has received so little attention and less “theoretical” treatment, time has been spent here on formulating it properly, deriving some basic equations, and emphasizing the overriding importance and effects of the design condition rather than generating solu-tions for many specific design situations. Essentially, any initial field for which the stress function is known can now be investigated and shapes derived of practical interest and importance. There are also a myriad of pos-sibilities and directions for further basic study. The exterior problem, ques-tions of existence and uniqueness, nonhomogeneous or nonisotropic materials, energy formulations, other design conditions, and related prob-lems in other areas of applied science are a few of the obvious possibilities.