Simple applications of Integral Calculus

Simple applications

So far in this section we have been using x as the variable of integration. In the case of applications, it is often convenient to use a different variable. For instance in the equation of motion the independent variable is time and the variable of integration is t.

In this section we discuss how integration is used to find the position and velocity of an object, given its acceleration and similar types of problems. Mathematically, this means that, starting with the derivative of a function, we must find the original function. Many common word which indicate derivative such as rate, growth, decay, marginal, change, varies, increase, decrease etc.

Example 11.10

If f ′(x ) = 3x2 − 4x + 5 and f (1) = 3, then find f (x) .

Solution

Given that f ′(x ) = dx/d ( f (x )) = 3x 2 − 4x + 5

Integrating on both sides with respect to x, we get

∫ f (x) dx(3x 2 4x 5) dx f (x )

f(x) = x 3 − 2x 2 + 5x + c

To determine the constant of integration c, we have to apply the given information f (1) = 3

f (1) = 3 ⇒ 3 = (1)3 − 2(1)2 + 5(1) + c ⇒ c = −1

Thus  f (x ) = x 3 − 2x 2 + 5x −1.

Example 11.11

A train started from Madurai Junction towards Coimbatore at 3pm (time t = 0) with velocity v(t ) = 20t + 50 kilometre per hour, where t is measured in hours. Find the distance covered by the train at 5pm.

Solution

In calculus terminology, velocity v = ds/dt is rate of change of position with time, where s is the distance.The velocity of the train is given by

v (t ) = 20t + 50

Therefore, ds /dt= 20t + 50

To find the distance function s one has to integrate the derivative function.

That is,  s = ∫( 20t + 50) dt

s= 10t 2 + 50t + c

The distance covered by the train is zero when time is zero. Let us use this initial condition s = 0 at t = 0 to determine the value c of the constant of integration.

⇒ s = 10t 2 + 50t + c ⇒ c = 0

Therefore, s = 10t 2 + 50t

The distance covered by the train in 2 hours (5pm-3pm) is given by substituting t = 2 in the above equation, we get

s= 10(2)2 + 50(2) = 140 km.

Example 11.12

The rate of change of weight of person w in kg with respect to their height h in centimetres is given approximately by dw/dh = 4.364×10−5 h2 . Find weight as a function of height. Also find the weight of a person whose height is 150 cm.

Solution

The rate of change of weight with respect to height

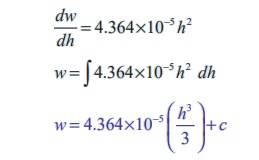
One can obviously understand that the weight of a person is zero when height is zero.

Let us find the value c of the constant of integration by substituting the initial condition w = 0, at h = 0 , in the above equation

When the height h = 150cm, the weight is w = 49kg (approximately)

Therefore, the weight of the person whose height 150cm is 49 kg.

Example 11.13

A tree is growing so that, after t - years its height is increasing at a rate of 18/√t cm per year.

Assume that when t = 0, the height is 5 cm.

(i) Find the height of the tree after 4 years.

(ii) After how many years will the height be 149 cm?

Solution

The rate of change of height h with respect to time t is the derivative of h with respect to t.

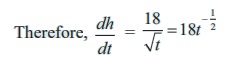
So, to get a general expression for the height, integrating the above equation with respect to t.

Thus after 16 years the height of the tree will be 149 cm.

Example 11.14

At a particular moment, a student needs to stop his speedy bike to avoid a collision with the barrier ahead at a distance 40 metres away from him. Immediately he slows (retardation)

the bike under braking at a rate of 8 metre/second 2 . If the bike is moving at a speed of 24m/s, when the brakes are applied, would it stop before collision?

Solution

Let a be the acceleration, v be the velocity of the car, and s be the distance.

Stated in calculus terminology, velocity, v = ds/dt , is the rate of change of position with time, and acceleration, a = dv/dt , is rate of change of velocity with time.

The acceleration to be negative because if you take the direction of movement to be positive, then for a bike that is slowing down, its acceleration vector will be oriented in the opposite direction of its motion (retardation).

Given that the retardation of the car is 8 meter/second2.

It is required to find the distance, not the velocity, so need more integration in order.

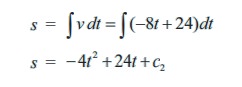
To determine c2 , the stopping distance s is measured from where, and when, the brakes are applied so that at t = 0, s = 0 .

s =  âˆ’ 4t 2 + 24t + c2 ⇒ 0 = − 4(0) 2 + 24(0) + c₂ ⇒ c2 =0

s =  âˆ’ 4t 2 + 24t

The stopping distance s could be evaluated if we knew the braking time. The time can be determined from the speed statement.

The bike stops when v = 0 , ⇒ v = −8t + 24 ⇒ 0 = −8t + 24 ⇒ t = 3.

When t = 3 , we get

s =  âˆ’ 4t 2 + 24t ⇒ s = − 4(3) 2 + 24(3)

s= 36 metres

The bike stops at a distance 4 metres to the barrier.

EXERCISE 11.4

(1) If f ′(x) = 4x − 5 and f (2) = 1, find f ( x).

(2)  If f ′(x) = 9x2 − 6x and f (0) = −3, find f ( x).

(3) If f ′′(x) = 12x − 6 and f (1) = 30, f ′(1) = 5 find f ( x).

(4) A ball is thrown vertically upward from the ground with an initial velocity of 39.2 m/sec. If the only force considered is that attributed to the acceleration due to gravity, find

(i) how long will it take for the ball to strike the ground?

(ii) the speed with which will it strike the ground? and

(iii) how high the ball will rise?

(5) A wound is healing in such a way that t days since Sunday the area of the wound has been

decreasing at a rate of – 3/(t+2)2 cm2 per day. If on Monday the area of the wound was 2 cm2

(i) What was the area of the wound on Sunday?

(ii) What is the anticipated area of the wound on Thursday if it continues to heal at the same rate?

Answers

Exercise 11.4 (1)2x²+ 5x +3 (2) 3(x³-x²-1) (3) 2x³-3x²+5x+2 (4) (i) 8 seconds (ii) 39.2 m/sec (iii) 78.4 m/sec (5) (i) 2.5 sq.cm (ii) 1.5 sq.cm