Chapter: 11th Mathematics : UNIT 11 : Integral Calculus
Properties of Integrals
Properties of Integrals
(1) If k is any constant, then Ōł½ kf ( x)dx k Ōł½f ( x)dx
(2) Ōł½ ( f1 (x) ┬▒ f2 (x))dx = Ōł½ f1 (x)dx ┬▒Ōł½ f2 (x)dx
Note 11.1
The above two properties can be combined and extended as
Ōł½ ( k1 f1 ( x ) ┬▒ k 2 f 2 ( x ) ┬▒ k 3 f 3 ( x ) ┬▒. . .┬▒ k n f n ( x )) dx
= k1 Ōł½ f1 ( x ) dx ┬▒ k 2 Ōł½ f 2 ( x ) dx ┬▒ k 3 Ōł½ f 3 ( x )dx ┬▒. . .┬▒ k n Ōł½ f n ( x ) dx.
That is, the integration of the linear combination of a finite number of functions is equal to the linear combination of their integrals
Example 11.8
Integrate the following with respect to x:
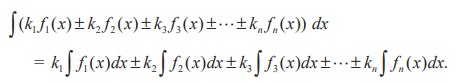


EXERCISE 11.3
Integrate the following with respect to x:
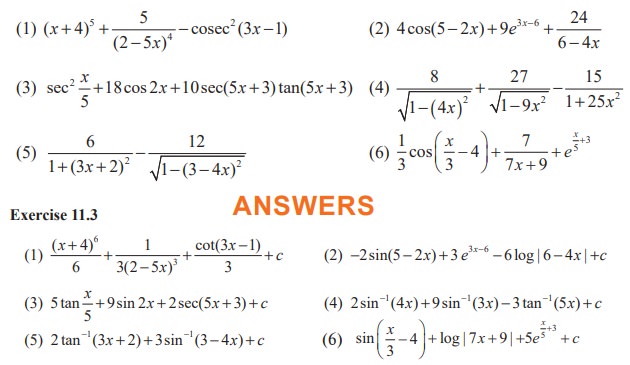
Related Topics