Methods of Integration

Methods of Integration

Integration is not as easy as differentiation. This is first due to its nature. Finding a derivative of a given function is facilitated by the fact that the differentiation itself has a constructive character. A derivative is simply defined as

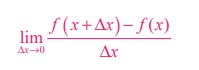
Suppose we are asked to find the derivative of log x, we know in all details how to proceed in order to obtain the result.

When we are asked to find the integral of log x, we have no constructive method to find integral or even how to start.

In the case of differentiation we use the laws of differentiation of several functions in order to find derivatives of their various combinations, like their sum, product, quotient, composition of functions etc.

There are very few such rules available in the theory of integration and their application is rather restricted. But the significance of these methods of integration is very great.

In every case one must learn to select the most appropriate method and use it in the most convenient form. This skill can only be acquired after long practice.

Already we have seen two important properties of integration. The following are the four important methods of integrations.

(1) Integration by decomposition into sum or difference.

(2) Integration by substitution.

(3) Integration by parts

(4) Integration by successive reduction.

Here we discuss only the first three methods of integration and the other will be studied in higher classes.