Newton Leibnitz Integral

Newton-Leibnitz Integral

Integral calculus is mainly divided into indefinite integrals and definite integrals. In this chapter, we study indefinite integration, the process of obtaining a function from its derivative.

We are already familiar with inverse operations. (+,-) (x,÷), ()n,n√ are some pairs of inverse operations. Similarly differentiation and integrations (d, ∫ ) are also inverse operations. In this section we develop the inverse operation of differentiation called ‘antidifferentiation’.

Definition 11.1

A function F (x) is called an antiderivative (Newton-Leibnitz integral or primitive) of a function f (x) on an interval I if

F ′(x ) = f (x) , for every value of x in I

Illustration 11.1

If F (x ) = x2 + 5 then

F ′(x ) = 2x .

Thus if f (x) is defined by

f( x ) = 2x, then

we say that f (x) is the derivative of F (x) and that F (x) is an antiderivative of f (x)

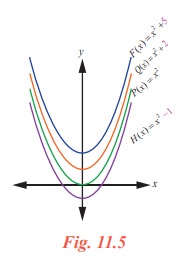
Consider the following table

We  can see  that the derivative  of F (x) , P (x) , Q (x) and H (x) is f (x) ,  but in  reverse the antiderivatives of f (x ) = 2x is not unique. That is the antiderivatives of f (x) is a family of infinitely many functions.

Theorem 11.1

If F (x) is a particular antiderivative of a function f (x) on an interval I, then every antiderivative of f (x) on I is given by

∫ f ( x)dx = F ( x) + c

where c is called an arbitrary constant, and all antiderivatives of f (x) on I can be obtained by assigning particular value to c.

The function f(x) is called Integrand.

The variable x in dx is called variable of integration or integrator.

The process of finding the integral is called integration or antidifferentiation (Newton-Leibnitz integral).

The peculiar integral sign ∫ originates in an elongated S (like Σ ) which stands for sum.

Often in applications involving differentiation it is desired to find a particular integral antiderivative that satisfies certain conditions called initial condition or boundary conditions.

For instance, if an equation involving dy/dx is given as well as the initial condition that y = y1 when x = x1, then after the set of all antiderivatives is found, if x and y are replaced by x1 and y1 , a particular value of the arbitrary constant is determined. With this value of c a particular antiderivative is obtained.

Illustration 11.2

Suppose we wish to find the particular antiderivative satisfying the equation

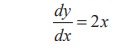
and the initial condition that y = 10 when x = 2.

From the given equation

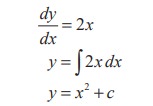
We substitute y = 10 when x = 2 , in the above equation

10 = 22 + c  â‡’  c = 6

When this value c =6 is substituted we obtain

= x2 + 6

which gives the particular antiderivative desired.