Equation, Solved Example Problems | Mathematics - Integration by parts | 11th Mathematics : UNIT 11 : Integral Calculus
Chapter: 11th Mathematics : UNIT 11 : Integral Calculus
Integration by parts
Integration by parts
Integration by parts method is generally used to find the integral when the integrand is a product of two different types of functions or a single logarithmic function or a single inverse trigonometric function or a function which is not integrable directly. From the formula for derivative of product of two functions we obtain this useful method of integration.
If u and v are two differentiable functions then we have
d (uv ) = vdu+udv
udv = d (uv ) - vdu
Integrating
Ōł½udv = Ōł½d (uv ) - Ōł½vdu
Ōł½udv = uv - Ōł½vdu
Ōł½udv in terms of another integral Ōł½vdu and does not give a final expression for the integral Ōł½udv. It only partially solves the problem of integrating the product u dv . Hence the term ŌĆśPartial IntegrationŌĆÖ has been used in many European countries. The term ŌĆ£Integration by PartsŌĆØ is used in many other countries as well as in our own.
The success of this method depends on the proper choice of u
(i) If integrand contains any non integrable functions directly from the formula, like logx, tanŌłÆ1 x etc., we have to take these non integrable functions as u and other as dv.
(ii) If the integrand contains both the integrable function, and one of these is xn (where n is a positive integer) then take u = xn.
(iii) For other cases the choice of u is ours.
Example 11.33
Evaluate the following integrals
(i) Ōł½xexdx
(ii) Ōł½ x cos x dx
(iii) Ōł½log x dx
(iv) Ōł½sinŌłÆ1x dx
Solution
(i) Let I = Ōł½ xe x dx.
Since x is an algebraic function and ex is an exponential function,
so take u = x then du = dx
dv = e x dx ŌćÆ v = ex
Applying Integration by parts, we get
Ōł½udv = uv ŌłÆ Ōł½vdu
ŌćÆ Ōł½ xex dx = xe x ŌłÆ Ōł½e x dx
That is, Ōł½ xe x dx = xe x ŌłÆ e x + c.
(ii) Let I = Ōł½ x cos x dx
Since x is an algebraic function and cos x is a trigonometric function,
so take u = x then du = dx
dv = cos xdx ŌćÆ v = sin x
Applying Integration by parts, we get
Ōł½udv = uv ŌłÆ Ōł½vdu
ŌćÆ Ōł½ x cos xdx = x sin x ŌłÆ Ōł½sin x dx
ŌćÆ Ōł½ x cos xdx = x sin x + cos x + c
(iii) Let I = Ōł½log x dx
Take u = log x then du = 1/x dx
dv = dx ŌćÆ v = x
Applying Integration by parts, we get
Ōł½udv = uv ŌłÆ Ōł½vdu
ŌćÆ log x dx = x log x ŌłÆ Ōł½x (1/x) dx
ŌćÆ Ōł½log x dx = x log x ŌłÆ x + c
(iv) Let I = Ōł½sinŌłÆ1x dx
u = sinŌłÆ1 (x), dv = dx
Then du = 1/ 1ŌłÆ x2 , v = x
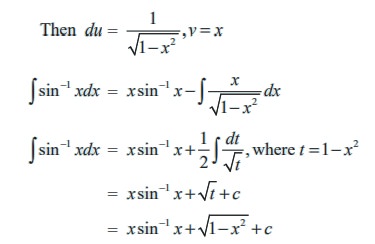

Related Topics