Integration of Rational Algebraic Functions

Integration of Rational Algebraic Functions

In this section we are going to discuss how to integrate the rational algebraic functions whose numerator and denominator contains some positive integral powers of x with constant coefficients.

Type I

Proof

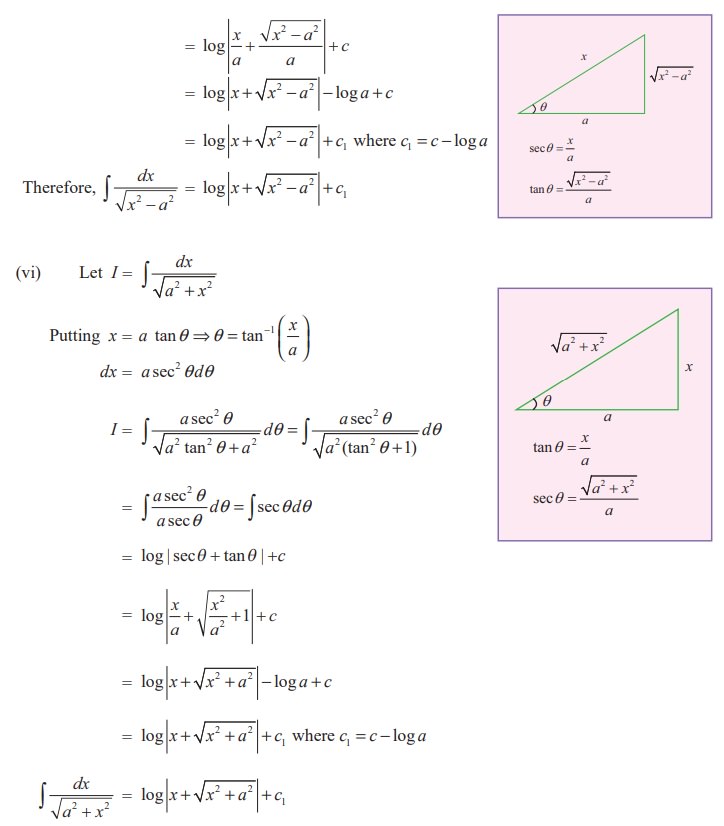
Remark: Remember the following useful substitution of the given integral as a functions of a2- x2 , a2 + x2 and x2 - a2.

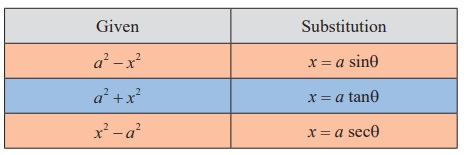
Type II

Integrals of the form

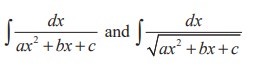
First we express ax 2 + bx + c as sum or difference of two square terms that is, any one of the forms to Type I. The following rule is used to express the expression ax2 + bx + c as a sum or difference of two square terms.

(1) Make the coefficient of x2 as unity.

(2) Completing the square by adding and subtracting the square of half of the coefficient of x.

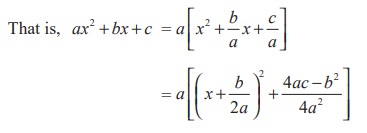
EXERCISE 11.10

Find the integrals of the following :

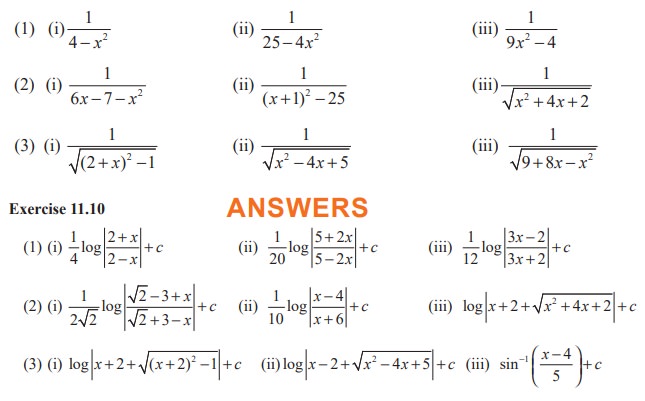
Type III

Integrals of the form

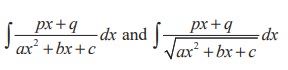
To evaluate the above integrals, first we write

px + q = A d/dx (ax 2 + bx + c ) + B

px + q = A(2ax + b ) + B

Calculate the values of A and B, by equating the coefficients of like powers of x on both sides

(i) The given first integral can be written as

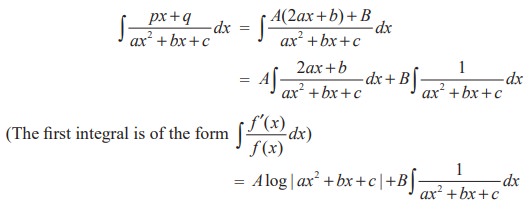
The second term on the right hand side can be evaluated using the previous types.

(ii) The given second integral can be written as

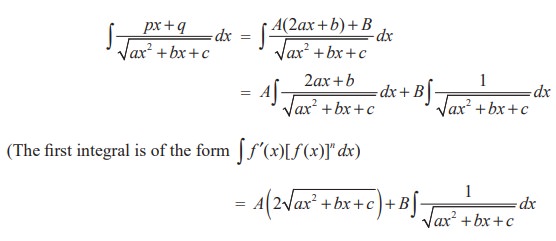
The second term on the right hand side can be evaluated using the previous types.

EXERCISE 11.11

Integrate the following with respect to x :

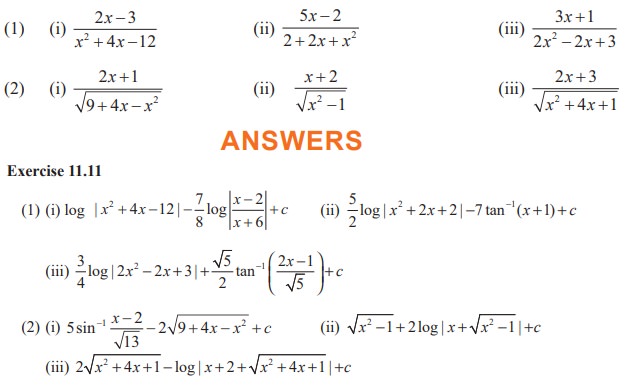
Type IV

Similarly we can prove other two results.

Note 11.3

The above problems can also be solved by substituting x= a sinθ

EXERCISE 11.12

Integrate the following functions with respect to x :