Equation, Solved Example Problems | Mathematics - Integrals of the form e pow(ax) cos bx and e pow(ax) sin bx | 11th Mathematics : UNIT 11 : Integral Calculus
Chapter: 11th Mathematics : UNIT 11 : Integral Calculus
Integrals of the form e pow(ax) cos bx and e pow(ax) sin bx
Integrals of the form
(i) Ōł½e ax ax sinbx dx (ii) Ōł½e ax cosbx dx
The following examples illustrate that there are some integrals whose integration continues forever. Whenever we integrate function of the form e axcos bx or eax sinbx, we have to apply the Integration by Parts rule twice to get the similar integral on both sides to solve.
Result 11.1


Caution
In applying integration by parts to specific integrals, the pair of choice for u and dv once initially assumed should be maintained for the successive integrals on the right hand side. (See the above two examples). The pair of choice should not be interchanged.
Examples 11.36
Evaluate the following integrals
(i) Ōł½e 3x cos 2x dx
(ii) Ōł½e ŌłÆ5x sin 3x dx
(i) Ōł½e 3x cos 2x dx
Using the formula

EXERCISE 11.8
Integrate the following with respect to x
(1) (i) eax cos bx (ii) e2 x sin x (iii) eŌłÆ x cos 2x
(2) (i) eŌłÆ3x sin 2x (ii) eŌłÆ4xsin 2x (iii) eŌłÆ3x cos x
Result 11.2
Ōł½ex [ f (x) + f ŌĆ▓(x)]dx = ex f (x) + c
Proof
Let I = Ōł½ex [ f (x) + f ŌĆ▓(x)]dx
= Ōł½ e x f (x)dx + Ōł½ex f ŌĆ▓(x)dx
Take u = f ( x); du = fŌĆÖ ( x) dx, in the first integral
dv = ex ;v = ex ,
That is, I = ex f (x) ŌłÆ Ōł½ e x f ŌĆ▓( x)dx + Ōł½ex f ŌĆ▓(x)dx + c
Therefore, I = e x f ( x ) + c.
EXERCISE 11.9
Integrate the following with respect to x:
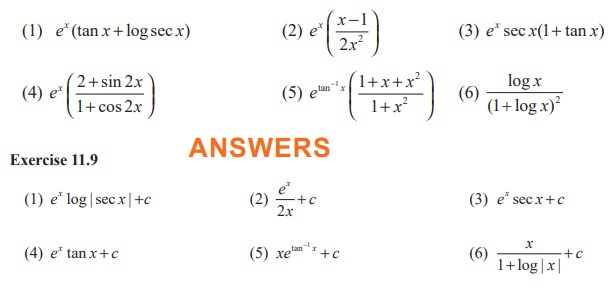
Related Topics
