Sensitivity Analysis with TORA, Solver, and AMPL

Sensitivity Analysis with TORA, Solver, and AMPL

We now have all the tools needed to decipher the output provided by LP software, particularly with regard to sensitivity analysis. We will use the TOYCO example to demon-strate the TORA, Solver, and AMPL output.

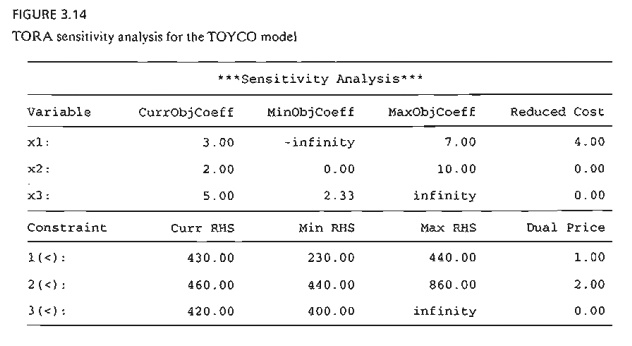
TORA's LP output report provides the sensitivity analysis data automatically as shown in Figure 3.14 (file toraTOYCO.txt). The output includes the reduced costs and the dual prices as well as their allowable optimality and feasibility ranges.

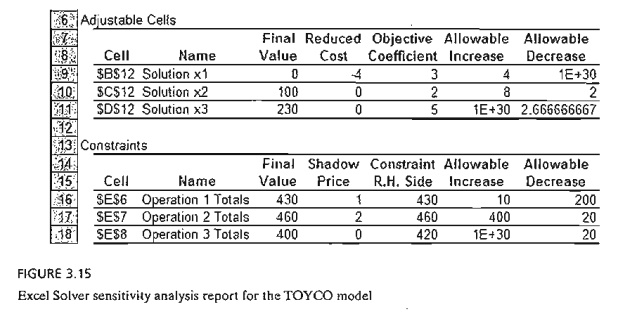
Figure 3.15 provides the Solver TOYCO model (file solverTOYCo.xls) and its sensitivity analysis report. After you click Solve in the Solvcr Parameters dialogue box, the new dialogue box Solver Rcsults will give you the opportunity to request further details about the solution, including the important sensitivity analysis report. The re-port will be stored in a separate Excel sheet, as shown by the choices on the bottom of the screen. You can then click Sensitivity Report 1 to view the results. The report is similar to TORA's with three exceptions: (1) The reduced cost carries an opposite sign. (2) The name shadow price replaces the name du.al price. (3) The optimality ranges are for the changes d_j and D_j rather than for the total objective coefficients and constraints on the right-hand side. The differences are minor and the interpretation of the results remains the same. 

In AMPL, the sensitivity analysis report is readily available. File amplTOYCo.txt provides the code necessary to determine the sensitivity analysis output. It requires the following additional statements:

The CPLEX option statements are needed to be able to obtain the standard sen-sitivity analysis report. In the TOYCO model, the indexed variables and constraints use the root names x and oper, respectively. Using these names, the suggestive suffixes . down, . current, and. up in the display statements automatically generate the for-matted sensitivity analysis report in Figure 3.16. The suffixes . dual and. rc provide the dual price and the reduced cost.

An alternative to AMPL's standard sensitivity analysis report is to actually solve the LP model for a range of values for the objective coefficients and the right-hand side of the constraints. AMPL automates this process through the use of commands (see Section A.7). Suppose in the TOYCO model, file amplTOYCo.txt, that we want to in-vestigate the effect of making changes in b [1] , the total available time for operation 1. We can do so by moving solve and display from amplTOYCO.txt to a new file, which we arbitrarily name analysis. txt:

The first line will provide the model and its data and the second line will provide the optimum solutions starting with b [II at 430 (the initial value given in amplTOYCO.txt) and continuing in increments of 1 until b [1] reaches 500. An examination of the out-put will then allow us to study the sensitivity of the optimum solution to changes in b [1]  Similar procedures can be followed with other coefficients including the case of making simultaneous changes.

PROBLEM SET 3.6E

1. Consider Problem 1, Set 2.3c (Chapter 2). Use the dual price to decide if it is worthwhile to increase the funding for year 4.

2. Consider Problem 2, Set 2.3c (Chapter 2).

a.     Use the dual prices to determine the overall return on investment.

b.     If you wish to spend $1000 on pleasure at the end of year 1, how would this affect the accumulated amount at the start of year 5?

1.     Consider Problem 3, Set 2.3c (Chapter 2).

a.     Give an economic interpretation of the dual prices of the model.

b.     Show how the dual price associated with the upper bound on borrowed money at the beginning of the third quarter can be derived from the dual prices associated with the balance equations representing the in-out cash flow at the five designated dates of the year.

2.     Consider Problem 4, Set 2.3c (Chapter 2). Use the dual prices to determine the rate of re-turn associated with each year.

*5. Consider Problem 5, Set 2.3c (Chapter 2). Use the dual price to determine if it is worth-while for the executive to invest more money in the plans.

6. Consider Problem 6, Set 2.3c (Chapter 2). Use the dual price to decide if it is advisable for the gambler to bet additional money.

7. Consider Problem 1, Set 2.3d (Chapter 2). Relate the dual prices to the unit production costs of the model.

8. Consider Problem 2, Set 2.3d (Chapter 2). Suppose that any additional capacity of ma-chines 1 and 2 can be acquired only by using overtime. What is the maximum cost per hour the company should be willing to incur for either machine?

*9.  Consider Problem 3, Set 2.3d (Chapter 2).

a.     Suppose that the manufacturer can purchase additional units of raw material A at $12 per unit. Would it be advisable to do so?

b.     Would you recommend that the manufacturer purchase additional units of raw ma-terial B at $5 per unit?

10. Consider Problem 10, Set 2.3e (Chapter 2).

a)     Which of the specification constraints impacts the optimum solution adversely?

b)    What is the most the company should pay per ton of each ore?