LP Model in Equation Form

LP MODEL IN EQUATION FORM

The development of the simplex method computations is facilitated by imposing two requirements on the constraints of the problem:

1. All the constraints (with the exception of the nonnegativity of the variables) are equations with nonnegative right-hand side.

2. All the variables are nonnegative.

These two requirements are imposed here primarily to standardize and streamline the simplex method calculations. It is important to know that all commercial packages (and TORA) directly accept inequality constraints, nonnegative right-hand side, and unrestricted variables. Any necessary preconditioning of the model is done internally in the software before the simplex method solves the problem.

1.1 Converting Inequalities into Equations with Nonnegative Right-Hand Side

In (≤) constraints, the right-hand side can be thought of as representing the limit on the availability of a resource, in which case the left-hand side would represent the usage of this limited resource by the activities (variables) of the model. The difference between the right-hand side and the left-hand side of the (≤) constraint thus yields the

unused or slack amount of the resource.

To convert a (≤)-inequality to an equation, a nonnegative slack variable is added to the left-hand side of the constraint. For example, in the Reddy Mikks model (Example 2.1-1), the constraint associated with the use of raw material M1 is given as

6x_l + 4x₂ ≤ 24

Defining s₁ as the slack or unused amount of MI, the constraint can be converted to the following equation:

6x₁ + 4x₂ + s₁ = 24, s₁ ≥0

Next, a (≥)-constraint sets a lower limit on the activities of the LP model, so that the amount by which the left-hand side exceeds the minimum limit represents a surplus. The conversion from (≥) to (=) is achieved by subtracting a nonnegative surplus variable from the left-hand side of the inequality. For example, in the diet model (Example 2.2-2), the constraint representing the minimum feed requirements is

x_l + x₂   ≥ 800

Defining s_l as the surplus variable, the constraint can be converted to the following equation

x₁ + x₂ - S_I = 800, S_l ≥ 0

The only remaining requirement is for the right-hand side of the resulting equation to be nonnegative. The condition can always be satisfied by multiplying both sides of the resulting equation by -1, where necessary. For example, the constraint

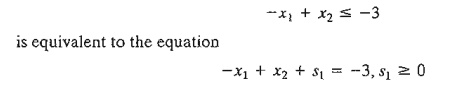
Now, multiplying both sides by -1 will render a nonnegative right-hand side, as de-sired-that is,

x_l - x₂ - S₁ = 3

2. Dealing with Unrestricted Variables

In Example 2.3-6 we presented a multiperiod production smoothing model in which the workforce at the start of each period is adjusted up or down depending on the demand for that period. Specifically, if x_i ( ≥ 0) is the workforce size in period i, then x_{i +l} (≥ 0) the workforce size in period i + 1 can be expressed as

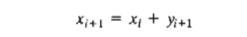
The variable y_i+l  must be unrestricted in sign to allow x_i+l to increase or decrease relative to x_i depending on whether workers are hired or fired, respectively.

As we will see shortly, the simplex method computations require all the variables be nonnegative. We can always account for this requirement by using the substitution

To show how this substitution works, suppose that in period 1 the workforce is x_l = 20 workers and that the workforce in period 2 will be increased by 5 to reach 25 workers. In terms of the variables 

The substitution also allows for the possibili-ty of no change in the workforce by letting both variables assume a zero value.

You probably are wondering about the possibility that both y₂⁺ and y₂^- may as-sume positive values simultaneously. Intuitively, as we explained in Example 2.3-6, this cannot happen, because it means that we can hire and fire a worker at the same time. This intuition is also supported by a mathematical proof that shows that, in any simplex method solution, it is impossible that both variables will assume positive values simultaneously.

PROBLEM SET 3.1 B

1. McBurger fast-food restaurant sells quarter-pounders and cheeseburgers. A quarter-pounder uses a quarter of a pound of meat, and a cheeseburger uses only .2 lb. The restaurant starts the day with 200 Ib of meat but may order more at an additional cost of 25 cents per pound to cover the delivery cost. Any surplus meat at the end of the day is donated to charity. McBurger's profits are 20 cents for a quarter-pounder and 15 cents for a cheeseburger. McBurger does not expect to sell more than 900 sandwiches in anyone day. How many of each type sandwich should McBurger plan for the day? Solve the problem using TORA, Solver, or AMPL.

2. Two products are manufactured in a machining center. The productions times per unit of products 1 and 2 are 10 and 12 minutes, respectively. The total regular machine time is 2500 minutes per day. In anyone day, the manufacturer can produce between 150 and 200 units of product 1, but no more than 45 units of product 2. Overtime may be used to meet the demand at an additional cost of $.50 per minute. Assuming that the unit profits for products 1 and 2 are $6.00 and $7.50, respectively, formulate the problem as an LP model, then solve with TORA, Solver, or AMPL to determine the optimum production level for each product as well as any overtime needed in the center.

*3. JoShop manufactures three products whose unit profits are $2, $5, and $3, respectively. The company has budgeted 80 hours of labor time and 65 hours of machine time for the production of three products. The labor requirements per unit of products 1,2, and 3 are 2, 1, and 2 hours, respectively. The corresponding machine-time requirements per unit are 1,1, and 2 hours. JoShop regards the budgeted labor and machine hours as goals that may be exceeded, if necessary, but at the additional cost of $15 per labor hour and $10 per ma-chine hour. Formulate the problem as an Lp, and determine its optimum solution using TORA, Solver, or AMPL.

4. In an LP in which there are several unrestricted variables, a transformation of the type