Chapter: Operations Research: An Introduction : The Simplex Method and Sensitivity Analysis
Graphical Sensitivity Analysis
SENSITIVITY ANALYSIS
In LP,
the parameters (input data) of the model can change within certain limits
with-out causing the optimum solution to change. This is referred to as sensitivity analysis, and will be the
subject matter of this section. Later, in Chapter 4, we will study post-optimal analysis which deals with
determining the new optimum solution resulting from making targeted changes in the input data.
In LP
models, the parameters are usually not exact. With sensitivity analysis, we can
ascertain the impact of this uncertainty on the quality of the optimum
solution. For example, for an estimated unit profit of a product, if
sensitivity analysis reveals that the optimum remains the same for a ±10%
change in the unit profit, we can conclude that the solution is more robust
than in the case where the indifference range is only ±1 %.
We will
start with the more concrete graphical solution to explain the basics of sensitivity
analysis. These basics will then be extended to the general LP problem using
the simplex tableau results.
1. Graphical Sensitivity Analysis
This
section demonstrates the general idea of sensitivity analysis. Two cases will
be considered:
1. Sensitivity
of the optimum solution to changes in the availability of the resources
(right-hand side of the constraints).
2. Sensitivity
of the optimum solution to changes in unit profit or unit cost (coefficients
of the objective function).
We will
consider the two cases separately, using examples of two-variable graphical
LPs.
Example 3.6-1 (Changes
in the Right-Hand Side)
JOBCO
produces two products on two machines. A unit of product 1 requires 2 hours on
machine 1 and 1 hour on machine 2. For product 2, a unit requires 1 hour on
machine 1 and 3 hours on ma-chine 2. The revenues per unit of products 1 and 2
are $30 and $20, respectively. The total daily processing time available for
each machine is 8 hours.
Letting xl
and x2
represent the daily number of units of products 1 and 2, respectively, the LP
model is given as
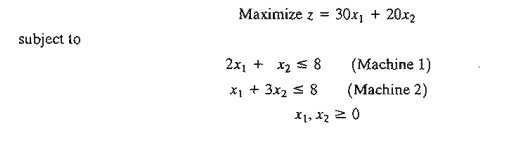
Figure
3.12 illustrates the change in the optimum solution when changes are made in
the capaci-ty of machine 1. If the
daily capacity is increased from 8 hours to 9 hours, the new optimum will occur
at point G. The rate of change in optimum z
resulting from changing machine 1 capacity from 8 hours to 9 hours can be
computed as follows:
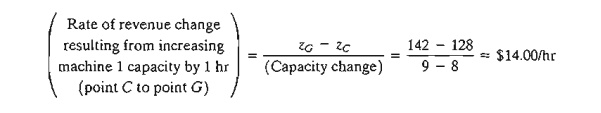
The
computed rate provides a direct link
between the model input (resources) and its output (total revenue) that
represents the unit worth of a resource
(in $/hr)-that is, the change in the optimal objective value per unit change in
the availability of the resource (machine capacity). This means that a unit
increase (decrease) in machine 1 capacity will increase (decrease) revenue by
$14.00. Although unit worth of a resource
is an apt description of the rate of change of the objective function, the
technical name dual or shadow price is now standard in the LP literature and
all software packages and, hence, will be used throughout the book.
FIGURE 3.12
Graphical
sensitivity of optimal solurion to changes in the availability of resources
(right-hand side of the constraints)
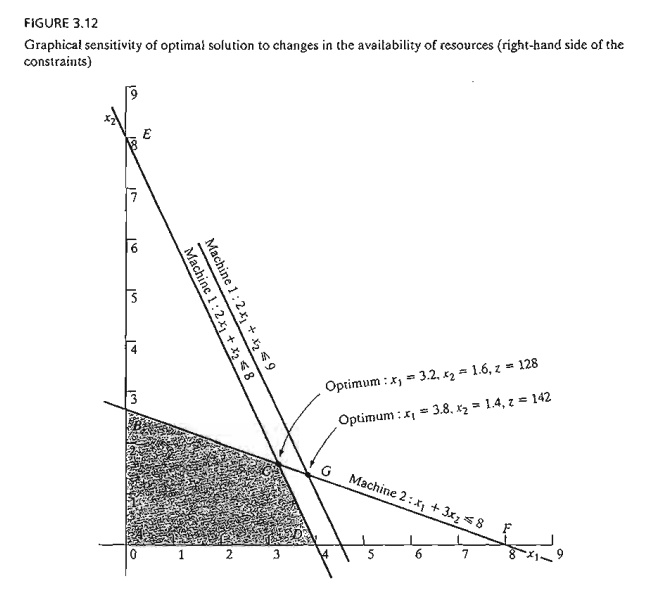
Looking
at Figure 3.12, we can see that the dual price of $14.00/hr remains valid for
changes (increases or decreases) in machine 1 capacity that move its constraint
parallel to itself to any point on the line segment BF. This means that the range of
applicability of the given dual price can be computed as follows:
Minimum
machine 1 capacity [at B = (0,2.67)]
= 2 x 0 + 1 x 2.67 = 2.67
hr
Maximum
machine 1 capacity [at F =(8,0)] = 2 x 8 + 1 x 0 =
16 hr
We can
thus conclude that the dual price of $14.00/hr will remain valid for the range
2.67 hrs ≤ Machine 1 capacity ≤ 16 hrs
Changes
outside this range will produce a different dual price (worth per unit).
Using
similar computations, you can verify that the dual price for machine 2 capacity
is $2.00/hr and it remains valid for changes (increases or decreases) that move
its constraint parallel to itself to any point on the line segment DE, which
yields the following limits:
Minimum
machine 2 capacity [at D = (4,0)] =
1 x 4 + 3 x a = 4 hr
Maximum
machine 2 capacity [at E = (8,
0)] = 1 x a + 3 x 8 = 24 hr
The
conclusion is that the dual price of $2.00/hr for machine 2 will remain
applicable for the range
4 hr ≤ Machine 2 capacity ≤ 24 hr
The
computed limits for machine 1 and 2 are referred to as the feasibility ranges.
All software packages provide information about the dual prices and their
feasibility ranges. Section 3.6.4 shows how AMPL, Solver, and TORA generate
this information.
The dual
prices allow making economic decisions about the LP problem, as the following
questions demonstrate:
Question 1. If JOBCO can increase the capacity of both machines, which machine should
receive higher priority?
The dual
prices for machines 1 and 2 are $14.00/hr and $2.00/hr. TIlis means that each
addi-tional hour of machine 1 will increase revenue by $14.00, as opposed to
only $2.00 for machine 2. Thus, priority should be given to machine 1.
Question 2. A suggestion is made to increase
the capacities of machines 1 and 2 at the addi-tional cost of $10/hr. Is this
advisable?
For
machine 1, the additional net revenue per hour is 14.00 - 10.00 = $4.00 and for
ma-chine 2, the net is $2.00 - $10.00 = -$8.00. Hence, only the capacity of
machine 1 should be increased.
Question 3. If the
capacity of machine 1 is increased from the present 8 hours to 13 hours, how
will this increase impact the optimum revenue?
The dual
price for machine 1 is $14.00 and is applicable in the range (2.67,16) hr. The
pro-posed increase to 13 hours falls within the feasibility range. Hence, the
increase in revenue is $14.00(13 - 8) = $70.00,
which means that the total revenue will be increased to (current revenue + change in revenue) = 128 + 70 = $198.00.
Question 4. Suppose that the capacity of
machine 1 is increased to 20 hours, how will this in-crease impact the optimum
revenue?
The
proposed change is outside the range (2.67, 16) hr for which the dual price of
$14.00 re-mains applicable. Thus, we can only make an immediate conclusion
regarding an increase up to 16 hours. Beyond that, further calculations are
needed to find the answer (see Chapter 4). Re-member that falling outside the
feasibility range does not mean that
the problem has no solution. It only
means that we do not have sufficient information to make an immediate decision.
Question 5. We know that the change in the
optimum objective value equals (dual price X change in resource) so long as the
change in the resource is within the feasibility range. What about the
associated optimum values of the variables?
The
optimum values of the variables will definitely change. However, the level of
informa-tion we have from the graphical solution is not sufficient to determine
the new values. Section 3.6.2, which treats the sensitivity problem
algebraically, provides this detail.
PROBLEM
SET 3.6A
1. A
company produces two products, A and B. The unit revenues are $2 and $3,
respective-ly. Two raw materials, M1 and M2, used in the manufacture of the
two products have re-spective daily availabilities of 8 and 18 units. One unit
of A uses 2 units of Ml and 2
units of M2, and 1 unit of Buses 3 units
of Ml and 6
units of M2.
a. Determine
the dual prices of Ml and M2 and their feasibility ranges.
b. Suppose that 4 additional units of
Ml can be acquired at the cost of 30 cents per unit. Would you recommend the
additional purchase?
c. What is the most the company should
pay per unit of M2?
d. If M2 availability is increased by
5 units, determine the associated optimum revenue.
*2. Wild
West produces two types of cowboy hats. A Type 1 hat requires twice as much
labor time as a Type 2. If all the
available labor time is dedicated to Type 2 alone, the company can produce a
total of 400 Type 2 hats a day. The respective market limits for the two types
are 150 and 200 hats per day. The revenue is $8 per Type 1 hat and $5 per Type
2 hat.
a. Use
the graphical solution to determine the number of hats of each type that
maxi-mizes revenue.
b. Determine
the dual price of the production capacity (in terms of the Type 2 hat) and the
range for which it is applicable.
c. If the daily demand limit on the
Type 1 hat is decreased to 120, use the dual price to determine the corresponding
effect on the optimal revenue.
d. What
is the dual price of the market share of the Type 2 hat? By how much can the
market share be increased while yielding the computed worth per unit?
Example
3.6-2 (Changes
in the Objective Coefficients)
Figure
3.13 shows the graphical solution space of the JOBCO problem presented in
Example 3.6-1. The optimum occurs at point C (xl == 3.2, x2
= 1.6, z == 128). Changes in revenue units (i.e., objective-function
coefficients) will change the slope of z.
However, as can be seen from the figure, the optimum solution will remain at
point C so long as the objective function lies between lines BF and DE, the two constraints that define the optimum point. This means
that there is a range for the coefficients of the objective function that will
keep the optimum solution un-changed at C.
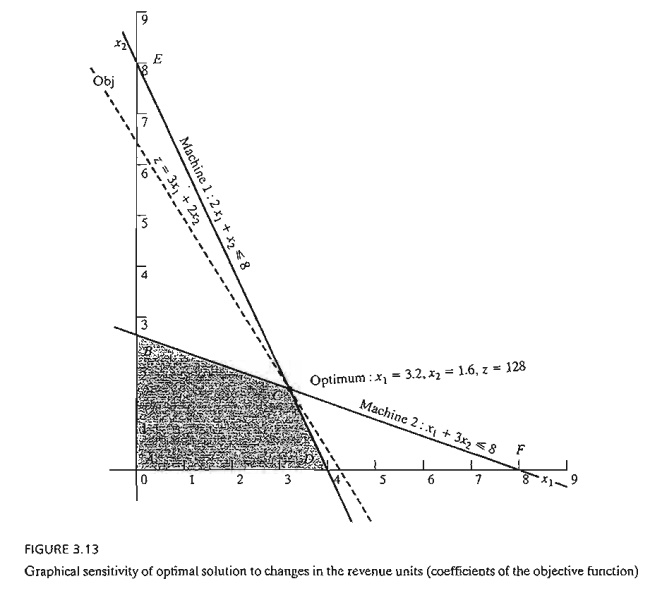
We can
write the objective function in the general format
Maximize
z =
Imagine
now that the line z is pivoted at C
and that it can rotate clockwise and counterclockwise. The optimum solution
will remain at point C so long as z = c1x1 + c2x2 lies
between the two lines xl + 3x2 = 8 and
2xl + x2 = 8.
This means that the ratio c1/c2 can vary
between 1/3 and 2/1, which yields the following
condition:
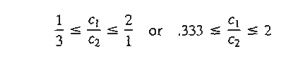
This
information can provide immediate answers regarding the optimum solution as the
follow-ing questions demonstrate:
Question 1. Suppose that the unit revenues
for products 1 and 2 are changed to $35 and $25, respectively. Will the current optimum remain the same?
The new
objective function is
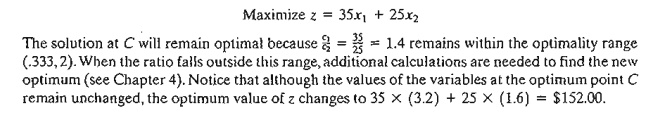
Question 2. Suppose that the unit revenue
of product 2 is fixed at its current value of c2 = $20.00.
What is the associated range for
Cj, the unit
revenue for product 1 that will keep the
optimum
unchanged?
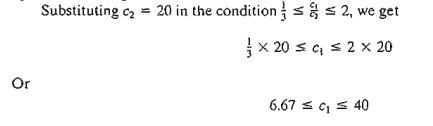
This
range is referred to as the optimality
range for c1 and it implicitly assumes that c2 is
fixed at $20.00.
We can
similarly determine the optimality range
for c2 by fixing the value of c1 at $30.00. Thus,

As in the
case of the right-hand side, all software packages provide the optimality
ranges. Section 3.6.4 shows how AMPL, Solver, and TORA generate these results.
Remark. Although the material in this
section has dealt only with two variables, the results lay the foundation for
the development of sensitivity analysis for the general LP problem in Sections
3.6.2 and 3.6.3.
PROBLEM SET 3.6B
1. Consider
Problem 1, Set 3.6a.
a. Determine
the optimality condition for cA/cB that
will keep the optimum unchanged.
b. Determine
the optimality ranges for cA and c8, assuming that the other
coefficient is kept constant at its present value.
c. If the unit revenues cA
and cB
are
changed simultaneously to $5 and $4, respectively, determine the new optimum
solution.
d. If the changes in (c) are made one
at a time, what can be said about the optimum solution?
2. In the
Reddy Mikks model of Example 2.2-1;
a. Determine
the range for the ratio of the unit revenue of exterior paint to the unit
revenue of interior paint.
b. If the revenue per ton of exterior
paint remains constant at $5000 per ton, determine the maximum unit revenue of interior
paint that will keep the present optimum solu-tion unchanged.
d. If for marketing reasons the unit
revenue of interior paint must be reduced to $3000, will the current optimum
production mix change?
*3. In
Problem 2, Set 3.6a:
a. Determine
the optimality range for the unit revenue ratio of the two types of hats that
will keep the current optimum unchanged.
b. Using
the information in (b), will the optimal solution change if the revenue per
unit is the same for both types?
Related Topics